
題目列表(包括答案和解析)
| 1 |
| 1-x |
| ∫ |
0 |
| ∫ |
0 |
| ∫ |
0 |
| ∫ |
0 |
| ∫ |
0 |
| 1 |
| 1-x |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| n+1 |
| 1 |
| 2 |
| C | 0 n |
| 1 |
| 2 |
| 1 |
| 2 |
| C | 1 n |
| 1 |
| 2 |
| 1 |
| 3 |
| C | 2 n |
| 1 |
| 2 |
| 1 |
| n+1 |
| C | n n |
| 1 |
| 2 |
| 1 |
| n+1 |
| 3 |
| 2 |
| 1 |
| n+1 |
| 3 |
| 2 |
已知函數 ,
, ,k為非零實數.
,k為非零實數.
(Ⅰ)設t=k2,若函數f(x),g(x)在區間(0,+∞)上單調性相同,求k的取值范圍;
(Ⅱ)是否存在正實數k,都能找到t∈[1,2],使得關于x的方程f(x)=g(x)在[1,5]上有且僅有一個實數根,且在[-5,-1]上至多有一個實數根.若存在,請求出所有k的值的集合;若不存在,請說明理由.
【解析】本試題考查了運用導數來研究函數的單調性,并求解參數的取值范圍。與此同時還能對于方程解的問題,轉化為圖像與圖像的交點問題來長處理的數學思想的運用。
已知數列{an}及fn(x)=a1x+a2x2+…+anxn, fn(-1)=(-1)nn,n=1,2,3,…,
(1)求 a1, a2, a3的值;
(2)求數列{an}的通項公式;
(3)求證: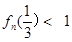 .
.
【解析】本試題主要是考查了數列中歸納猜想的原理,意義運用函數關系求解數列的通項公式,并且運用錯位相減法求解數列的和的數學思想。

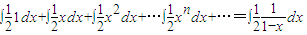
 .
. = .
= .某電視臺曾有一檔娛樂節目,主持人會給選手在限定時間內猜某一物品售價的機會,如果猜中,就把物品獎勵給選手,某次猜一種品牌的手機,手機價格在500~1 000元之間.選手開始報價1 000元,主持人說:高了;緊接著報價900元,高了;700元,低了;800元,低了;880元,高了;850元,低了;851元,恭喜你,你猜中了.表面上看,猜價格具有很大的碰運氣的成分;實際上,游戲報價的過程體現了“逼近”的數學思想.你能設計出可行的猜價方案來幫助選手猜價嗎?
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com