
題目列表(包括答案和解析)
平面直角坐標系內的向量都可以用一有序實數對唯一表示,這使我們想到可以用向量作為解析幾何的研究工具.如圖,設直線
l的傾斜角為α(α≠90°).在l上任取兩個不同的點 ,
, ,不妨設向量
,不妨設向量 的方向是向上的,那么向量
的方向是向上的,那么向量 的坐標是(
的坐標是( ).過原點作向量
).過原點作向量 ,則點P的坐標是(
,則點P的坐標是( ),而且直線OP的傾斜角也是α.根據正切函數的定義得
),而且直線OP的傾斜角也是α.根據正切函數的定義得
 ,
,
這就是《數學
2》中已經得到的斜率公式.上述推導過程比《數學2》中的推導簡捷.你能用向量作為工具討論一下直線的有關問題嗎?例如:(1)
過點 ,平行于向量
,平行于向量 的直線方程;
的直線方程;
(2)
向量(A,B)與直線 的關系;
的關系;
(3)
設直線 和
和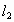 的方程分別是
的方程分別是
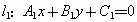

那么,
 ∥
∥ ,
, 的條件各是什么?如果它們相交,如何得到它們的夾角公式?
的條件各是什么?如果它們相交,如何得到它們的夾角公式?
(4)
點 到直線
到直線 的距離公式如何推導?
的距離公式如何推導?

 將邊長為1的正三角形ABC按如圖所示的方式放置,其中頂點A與坐標原點重合.記邊AB所在直線的傾斜角為θ,已知
將邊長為1的正三角形ABC按如圖所示的方式放置,其中頂點A與坐標原點重合.記邊AB所在直線的傾斜角為θ,已知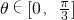 .
. 的坐標(要求將結果化簡為形如(cosα,sinα)的形式);
的坐標(要求將結果化簡為形如(cosα,sinα)的形式); .
. 的坐標(要求將結果化簡為形如(cosα,sinα)的形式);
的坐標(要求將結果化簡為形如(cosα,sinα)的形式);
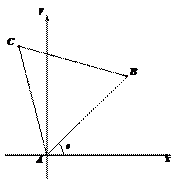 將邊長為1的正三角形
將邊長為1的正三角形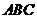 按如圖所示的方式放置,其中頂點
按如圖所示的方式放置,其中頂點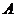 與坐標原點重合.記邊
與坐標原點重合.記邊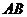 所在直線的傾斜角為
所在直線的傾斜角為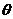 ,已知
,已知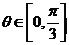 .
.
(Ⅰ)試用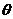 表示
表示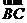 的坐標(要求將結果化簡為形如
的坐標(要求將結果化簡為形如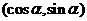 的形式);
的形式);
(Ⅱ)定義:對于直角坐標平面內的任意兩點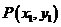 、
、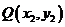 ,稱
,稱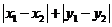 為
為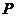 、
、 兩點間的“taxi距離” ,并用符號
兩點間的“taxi距離” ,并用符號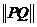 表示.試求
表示.試求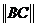 的最大值.
的最大值.
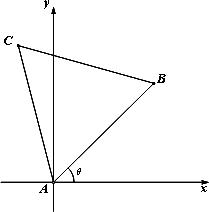
將邊長為1的正三角形ABC按如圖所示的方式放置,其中頂點A與坐標原點重合.記邊AB所在直線的傾斜角為![]() ,已知
,已知![]() ∈[0,
∈[0,![]() ].
].
(Ⅰ)試用![]() 表示
表示![]() 的坐標(要求將結果化簡為形如(cosα,sinα)的形式);
的坐標(要求將結果化簡為形如(cosα,sinα)的形式);
(Ⅱ)定義:對于直角坐標平面內的任意兩點P(x1,y1)、Q(x2,y2),稱|x1-x2|+|y1-y2|為P、Q兩點間的“taxi距離”,并用符號||PQ||表示.試求||BC||的最大值.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com