
題目列表(包括答案和解析)
在解決問題:“證明數集 沒有最小數”時,可用反證法證明.
沒有最小數”時,可用反證法證明.
假設 是
是 中的最小數,則取
中的最小數,則取 ,可得:
,可得: ,與假設中“
,與假設中“ 是
是 中的最小數”矛盾! 那么對于問題:“證明數集
中的最小數”矛盾! 那么對于問題:“證明數集 沒有最大數”,也可以用反證法證明.我們可以假設
沒有最大數”,也可以用反證法證明.我們可以假設 是
是 中的最大數,則可以找到
中的最大數,則可以找到 ▲ (用
▲ (用 ,
, 表示),由此可知
表示),由此可知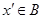 ,
, ,這與假設矛盾!所以數集
,這與假設矛盾!所以數集 沒有最大數.
沒有最大數.
| a+2 |
| 2 |
| 2+2 |
| 2 |
| a+2 |
| 2 |
| a+a |
| 2 |
| n |
| m |
| n0 |
| m0 |
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com