可以證明,對任意的n∈N*,有(1+2+…+n)2=13+23+…+n3成立.下面嘗試推廣該命題:
(1)設由三項組成的數列a1,a2,a3每項均非零,且對任意的n∈{1,2,3}有(a1+a2+…+an)2=a13+a23+…+an3成立,求所有滿足條件的數列;
(2)設數列{an}每項均非零,且對任意的n∈N*有(a1+a2+…+an)2=a13+a23+…+an3成立,數列{an}的前n項和為Sn.求證:an+12-an+1=2Sn,n∈N*;
(3)是否存在滿足(2)中條件的無窮數列{an},使得a2012=-2011?若存在,寫出一個這樣的無窮數列(不需要證明它滿足條件); 若不存在,說明理由.
【答案】
分析:(1)利用(a
1+a
2+…+a
n)
2=a
13+a
23+…+a
n3,分別取n=1,2,3代入求解即可;
(2)由已知當n≥2時,a
13+a
23+…+a
n3=S
n2,a
13+a
23+…+a
n-13=S
n-12,兩式相減,化簡可證;
(3)存在,
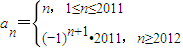
是一個滿足條件的無窮數列.
解答:解:(1)取n=1有a
12=a
13,又a
1≠0,∴a
1=1
取n=2,有(1+a
2)
2=1+a
23,∴a
2=-1或2
當a
2=-1時,同理得a
3=1;
當a
2=2時,同理得a
3=3或-2
綜上知,所有滿足條件思維數列為1,-1,1;1,2,3;1,2,-2.
(2)由已知當n≥2時,a
13+a
23+…+a
n3=S
n2,
a
13+a
23+…+a
n-13=S
n-12,
兩式相減知:a
n3=S
n2-S
n-12=a
n(2a
1+2a
2+…+2a
n-1+a
n),
∵a
n>0
∴a
n2=2a
1+2a
2+…+2a
n-1+2a
n-a
n∴a
n2=2S
n-a
n∴a
n+12-a
n+1=2S
n,n∈N
*;
(3)存在,
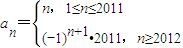
是一個滿足條件的無窮數列.
點評:本題以已知命題為前提,嘗試推廣新命題,考查賦值法.在解答的過程當中充分體現了數列通項與前n項和的知識.

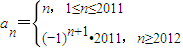 是一個滿足條件的無窮數列.
是一個滿足條件的無窮數列.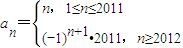 是一個滿足條件的無窮數列.
是一個滿足條件的無窮數列.

