日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

  (2005年上海高考題)用n個不同的實數a₁，a₂，…，a_n可得n!個不同的排列，每個排列為一行寫成一個n!行的數陣．對第i行a_i1，a_i2，…，a_in，記b_i＝－a_i1＋2a_i2－3a_i3＋…＋(－1)ⁿna_in，i＝1，2，3，…，n!．用1，2，3可得數陣如右，由于此數陣中每一列各數之和都是12，所以，b₁＋b₂＋┄＋b₆＝－12＋2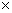12－3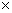12＝－24．那么，在用1，2，3，4，5形成的數陣中，b₁＋b₂＋┄＋b₁₂₀等于                                                                                                           

   A．－3600          B．1800        C．－1080        D．－720

(2005遼寧，9)若直線2x－y＋c=0按向量a=(1，－1)平移后與圓相切，則c的值為

[　　]

(2005遼寧，7)在R上定義運算．若不等式對任意實數x成立，則

[　　]

(2005遼寧，8)若鈍角三角形三內角的度數成等差數列，且最大邊長與最小邊長的比值為m，則m的范圍是

[　　]

(2005遼寧，10)已知y=f(x)是定義在R上的單調函數，實數，λ≠1，，，若，則

[　　]