例1. 在處可導.則 思路: 在處可導.必連續 ∴ ∴ 例2.已知f(x)在x=a處可導.且f′(a)=b.求下列極限: (1), (2) 分析:在導數定義中.增量△x的形式是多種多樣.但不論△x選擇哪種形式.△y也必須選擇相對應的形式.利用函數f(x)在處可導的條件.可以將已給定的極限式恒等變形轉化為導數定義的結構形式. 解:(1) (2) 說明:只有深刻理解概念的本質.才能靈活應用概念解題.解決這類問題的關鍵是等價變形.使極限式轉化為導數定義的結構形式. 例3.觀察...是否可判斷.可導的奇函數的導函數是偶函數.可導的偶函數的導函數是奇函數. 解:若為偶函數 令 ∴ 可導的偶函數的導函數是奇函數 另證: ∴ 可導的偶函數的導函數是奇函數 例4.(1)求曲線在點(1.1)處的切線方程, (2)運動曲線方程為.求t=3時的速度. 分析:根據導數的幾何意義及導數的物理意義可知.函數y=f(x)在處的導數就是曲線y=f(x)在點處的切線的斜率.瞬時速度是位移函數S(t)對時間的導數. 解:(1). .即曲線在點(1.1)處的切線斜率k=0 因此曲線在(1.1)處的切線方程為y=1 (2) . 例5. 求下列函數單調區間 (1) (2) (3) (4) 解:(1) 時 ∴ . (2) ∴ . (3) ∴ ∴ . . (4) 定義域為 例6.求證下列不等式 (1) (2) (3) 證:(1) ∴ 為上 ∴ 恒成立 ∴ ∴ 在上 ∴ 恒成立 (2)原式 令 ∴ ∴ ∴ (3)令 ∴ ∴ 例7.利用導數求和: (1), (2). 分析:這兩個問題可分別通過錯位相減法及利用二項式定理來解決.轉換思維角度.由求導公式.可聯想到它們是另外一個和式的導數.利用導數運算可使問題的解決更加簡捷. 解:(1)當x=1時. , 當x≠1時. ∵. 兩邊都是關于x的函數.求導得 即 (2)∵. 兩邊都是關于x的函數.求導得. 令x=1得 . 即. 例8.設.求函數的單調區間. 分析:本小題主要考查導數的概念和計算.應用導數研究函數性質的方法及推理和運算能力. 解:. 當時 . (i)當時.對所有.有. 即.此時在內單調遞增. (ii)當時.對.有. 即.此時在(0.1)內單調遞增.又知函數在x=1處連續.因此. 函數在(0.+)內單調遞增 (iii)當時.令.即. 解得. 因此.函數在區間內單調遞增.在區間 內也單調遞增. 令.解得. 因此.函數在區間內單調遞減. 例9.已知拋物線與直線y=x+2相交于A.B兩點.過A.B兩點的切線分別為和. (1)求A.B兩點的坐標, (2)求直線與的夾角. 分析:理解導數的幾何意義是解決本例的關鍵. 解 (1)由方程組 解得 A (2)由y′=2x.則..設兩直線的夾角為θ.根據兩直線的夾角公式. 所以 說明:本例中直線與拋物線的交點處的切線.就是該點處拋物線的切線.注意兩條直線的夾角公式有絕對值符號. 例10.設.是上的偶函數. (I)求的值, (II)證明在上是增函數. 解:(I)依題意.對一切有.即. ∴對一切成立. 由此得到.. 又∵.∴. (II)證明:由.得. 當時.有.此時.∴在上是增函數. 【
查看更多】
題目列表(包括答案和解析)
函數
f(x)在 處可導,則
處可導,則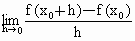
[
]
A
.與 、h都有關
、h都有關
B
.僅與 有關,而與h無關
有關,而與h無關
C
.僅與h有關,而與 無關
無關
D
.與 、h均無關
、h均無關
查看答案和解析>>
主站蜘蛛池模板:
91极品在线
|
一级免费毛片
|
国产精品免费一区二区三区都可以
|
日本精品在线播放
|
一区二区中文
|
日韩精品无玛区免费专区又长又大
|
精品成人佐山爱一区二区
|
国产在线小视频
|
人人草人人
|
久久高清一区
|
黄网站免费在线
|
久久中文字幕电影
|
99在线免费视频
|
av福利在线观看
|
91久久爽久久爽爽久久片
|
成人黄色大片
|
高清av一区
|
欧美日韩黄色一级片
|
久久久婷婷
|
久久亚洲网
|
99精品电影|
日韩在线视频精品
|
www.国产欧美
|
一本色道亚洲精品aⅴ
|
欧美一区二区三区在线看
|
亚洲国产精品久久精品怡红院
|
精品在线免费播放
|
国产一区二区久久久
|
激情视频网站
|
国产伦精品一区二区三区电影
|
欧美一级性|
国产精品一二三区
|
黄色免费在线观看
|
国产超碰人人爽人人做人人爱
|
中文字幕在线一区
|
国产亚洲综合精品
|
国产一区二区精品在线观看
|
欧美一区二区在线观看
|
成人精品一区二区三区电影黑人
|
日韩中文字幕在线观看
|
男人天堂社区
|

 在
在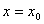 處可導,則
處可導,則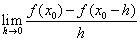 等于
等于  B.
B. C.
C. D.0
D.0![]() 在
在![]() 處可導,則
處可導,則![]() 等于
等于 ![]() B.
B.![]() C.
C.![]() D.
D.![]()
![]() 在
在![]() 處可導,且
處可導,且![]() ,則
,則![]()
![]() 在
在![]() 處可導,且
處可導,且![]() ,則
,則![]()
 處可導,則
處可導,則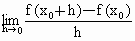
 、h都有關
、h都有關
 有關,而與h無關
有關,而與h無關
 無關
無關
 、h均無關
、h均無關