
題目列表(包括答案和解析)
已知橢圓
 的離心率為
的離心率為 ,以原點為圓心,橢圓的短半軸長為半徑的圓與直線
,以原點為圓心,橢圓的短半軸長為半徑的圓與直線 相切.
相切.
(I)求橢圓 的方程;
的方程;
(II)若過點 (2,0)的直線與橢圓
(2,0)的直線與橢圓 相交于兩點
相交于兩點 ,設
,設 為橢圓上一點,且滿足
為橢圓上一點,且滿足 (O為坐標原點),當
(O為坐標原點),當 <
< 時,求實數
時,求實數 的取值范圍.
的取值范圍.
【解析】本試題主要考查了橢圓的方程以及直線與橢圓的位置關系的運用。
第一問中,利用
第二問中,利用直線與橢圓聯系,可知得到一元二次方程中 ,可得k的范圍,然后利用向量的
,可得k的范圍,然后利用向量的 <
< 不等式,表示得到t的范圍。
不等式,表示得到t的范圍。
解:(1)由題意知

如圖,已知圓錐體 的側面積為
的側面積為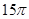 ,底面半徑
,底面半徑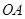 和
和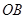 互相垂直,且
互相垂直,且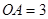 ,
, 是母線
是母線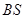 的中點.
的中點.

(1)求圓錐體的體積;
(2)異面直線 與
與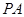 所成角的大小(結果用反三角函數表示).
所成角的大小(結果用反三角函數表示).
【解析】本試題主要考查了圓錐的體積和異面直線的所成的角的大小的求解。
第一問中,由題意, 得
得 ,故
,故
從而體積 .2中取OB中點H,聯結PH,AH.
.2中取OB中點H,聯結PH,AH.
由P是SB的中點知PH//SO,則 (或其補角)就是異面直線SO與PA所成角.
(或其補角)就是異面直線SO與PA所成角.
由SO 平面OAB,
平面OAB, PH
PH 平面OAB,PH
平面OAB,PH AH.在
AH.在 OAH中,由OA
OAH中,由OA OB得
OB得 ;
;
在 中,
中, ,PH=1/2SB=2,
,PH=1/2SB=2, ,
,
則 ,所以異面直線SO與P成角的大arctan
,所以異面直線SO與P成角的大arctan
解:(1)由題意, 得
得 ,
,
故 從而體積
從而體積 .
.
(2)如圖2,取OB中點H,聯結PH,AH.
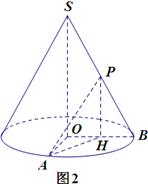
由P是SB的中點知PH//SO,則 (或其補角)就是異面直線SO與PA所成角.
(或其補角)就是異面直線SO與PA所成角.
由SO 平面OAB,
平面OAB, PH
PH 平面OAB,PH
平面OAB,PH AH.
AH.
在 OAH中,由OA
OAH中,由OA OB得
OB得 ;
;
在 中,
中, ,PH=1/2SB=2,
,PH=1/2SB=2, ,
,
則 ,所以異面直線SO與P成角的大arctan
,所以異面直線SO與P成角的大arctan
如圖,三棱柱 中,側棱垂直底面,∠ACB=90°,AC=BC=AA1,D是棱AA1的中點。
中,側棱垂直底面,∠ACB=90°,AC=BC=AA1,D是棱AA1的中點。

(I) 證明:平面 ⊥平面
⊥平面
(Ⅱ)平面 分此棱柱為兩部分,求這兩部分體積的比.
分此棱柱為兩部分,求這兩部分體積的比.
【命題意圖】本題主要考查空間線線、線面、面面垂直的判定與性質及幾何體的體積計算,考查空間想象能力、邏輯推理能力,是簡單題.
【解析】(Ⅰ)由題設知BC⊥ ,BC⊥AC,
,BC⊥AC, ,∴
,∴ 面
面 , 又∵
, 又∵
 面
面 ,∴
,∴ ,
,
由題設知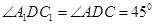 ,∴
,∴ =
= ,即
,即 ,
,
又∵ , ∴
, ∴ ⊥面
⊥面 , ∵
, ∵
 面
面 ,
,
∴面 ⊥面
⊥面 ;
;
(Ⅱ)設棱錐 的體積為
的體積為 ,
, =1,由題意得,
=1,由題意得, =
= =
= ,
,
由三棱柱 的體積
的體積 =1,
=1,
∴ =1:1, ∴平面
=1:1, ∴平面 分此棱柱為兩部分體積之比為1:1
分此棱柱為兩部分體積之比為1:1
已知正數數列{an }中,a1 =2.若關于x的方程 (
( )對任意自然數n都有相等的實根.
)對任意自然數n都有相等的實根.
(1)求a2 ,a3的值;
(2)求證
【解析】(1)中由題意得△ ,即
,即 ,進而可得
,進而可得 ,.
,.
(2)中由于 ,所以
,所以 ,因為
,因為 ,所以數列
,所以數列 是以
是以 為首項,公比為2的等比數列,知數列
為首項,公比為2的等比數列,知數列 是以
是以 為首項,公比為
為首項,公比為 的等比數列,利用裂項求和得到不等式的證明。
的等比數列,利用裂項求和得到不等式的證明。
(1)由題意得△ ,即
,即 ,進而可得
,進而可得
(2)由于 ,所以
,所以 ,因為
,因為 ,所以數列
,所以數列 是以
是以 為首項,公比為2的等比數列,知數列
為首項,公比為2的等比數列,知數列 是以
是以 為首項,公比為
為首項,公比為 的等比數列,于是
的等比數列,于是
 ,
,
所以
在等比數列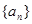 中,
中,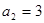 ,
,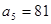 ;
;
(1)求數列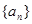 的通項公式;
(2)求數列
的通項公式;
(2)求數列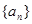 的前
的前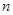 項和
項和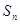
【解析】第一問中利用等比數列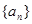 中,
中,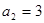 ,
,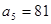 兩項確定通項公式即可
兩項確定通項公式即可
第二問中,在第一問的基礎上,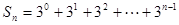 然后求和。
然后求和。
解:(1)由題意得到: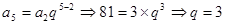
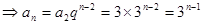 ……6分
……6分
(2) 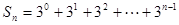 ……①
……①
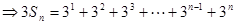 …… ②
…… ②
①-②得到 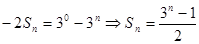
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com