日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

（本題滿分12分）

今天你低碳了嗎？近來，國內網站流行一種名為“碳排放計算器”的軟件，人們可以由此計算出自己每天的碳排放量。例如：家居用電的碳排放量（千克） = 耗電度數0.785，汽車的碳排放量（千克）=油耗公升數0.785等。某班同學利用寒假在兩個小區逐戶進行了一次生活習慣是否符合低碳觀念的調查。若生活習慣符合低碳觀念的稱為“低碳族”，否則稱為“非低碳族”。這二族人數占各自小區總人數的比例P數據如下：

（I）如果甲、乙來自A小區，丙、丁來自B小區，求這4人中恰有2人是低碳族的概率；

（II）A小區經過大力宣傳，每周非低碳族中有20%的人加入到低碳族的行列。如果2周后隨機地從A小區中任選25人，記表示25個人中低碳族人數，求E。

(本小題滿分12分) 某高校在2010年的自主招生考試成績中隨機抽取100名學生的筆試成績，按成績分組，得到的頻率分布表如下左圖所示.

（I）為了能選拔出最優秀的學生，高校決定在筆試成績高的第3、4、5組中用分層抽樣抽取6名學生進入第二輪面試，求第3、4、5組每組各抽取多少名學生進入第二輪面試？

（II）在（I）的前提下，學校決定在這6名學生中，隨機抽取2名學生接受A考官進行面試，求第4組至少有一名學生被考官A面試的概率？

( 本小題滿分12分)

甲、乙兩位學生參加數學競賽培訓．現分別從他們在培訓期間參加的若干次預賽成績中隨機抽取8次．記錄如下：

甲：82 81 79 78 95 88 93 84     乙：92 95 80 75 83 80 90 85

  （I）畫出甲、乙兩位學生成績的莖葉圖，指出學生乙成績的中位數；

（II）現要從中選派一人參加數學競賽，從平均狀況和方差的角度考慮，你認為派哪位學生參加合適?請說明理由；

（III）若將頻率視為概率，對學生甲在今后的三次數學競賽成績進行預測，記這三次成績中高于80分的次數為，求的分布列及數學期望.

( 本小題滿分12分)

甲、乙兩位學生參加數學競賽培訓．現分別從他們在培訓期間參加的若干次預賽成績中隨機抽取8次．記錄如下：

甲：82 81 79 78 95 88 93 84     乙：92 95 80 75 83 80 90 85

  （I）畫出甲、乙兩位學生成績的莖葉圖，指出學生乙成績的中位數；

（II）現要從中選派一人參加數學競賽，從平均狀況和方差的角度考慮，你認為派哪位學生參加合適?請說明理由；

（III）若將頻率視為概率，對學生甲在今后的三次數學競賽成績進行預測，記這三次成績中高于80分的次數為，求的分布列及數學期望.

（本小題滿分12分）某校舉行環保知識大獎賽，比賽分初賽和決賽兩部分，初賽采用選手選一題答一題的方式進行，每位選手最多有5次選題答題的機會，選手累計答對3題或答錯3題即終止其初賽的比賽，答對3題者直接進入決賽，答錯3題者則被淘汰，已知選手甲答題連續兩次答錯的概率為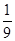，（已知甲回答每個問題的正確率相同，并且相互之間沒有影響。）（I）求甲選手回答一個問題的正確率；（Ⅱ）求選手甲可進入決賽的概率；（Ⅲ）設選手甲在初賽中答題的個數為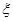，試寫出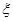的分布列，并求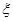的數學期望。