
題目列表(包括答案和解析)
(本小題滿分12分)已知函數 是定義在
是定義在 上的奇函數,且
上的奇函數,且 ,
,
(1)確定函數 的解析式;
的解析式;
(2)用定義證明 在
在 上是增函數;
上是增函數;
(3)解不等式 .
.
【解析】第一問利用函數的奇函數性質可知f(0)=0
結合條件 ,解得函數解析式
,解得函數解析式
第二問中,利用函數單調性的定義,作差變形,定號,證明。
第三問中,結合第二問中的單調性,可知要是原式有意義的利用變量大,則函數值大的關系得到結論。
 閱讀以下程序語句,若希望輸出s=55,則應將條件i≥8改為
閱讀以下程序語句,若希望輸出s=55,則應將條件i≥8改為(本小題滿分12分)有一批貨物需要用汽車從城市甲運至城市乙,已知從城市甲到城市乙只有兩條公路,且通過這兩條公路所用的時間互不影響.據調查統計,通過這兩條公路從城市甲到城市乙的200輛汽車所用時間的頻數分布如下表:所用的時間(天數)

(I)為進行某項研究,從所用時間為12天的60輛汽車中隨機抽取6輛.
(i) 若用分層抽樣的方法抽取,求從通過公路1和公路2的汽車中各抽取幾輛;
(ii)若從(i)的條件下抽取的6輛汽車中,再任意抽取兩輛汽車,求這兩輛汽車至少有一輛通過公路1的概率.
(II)假設汽車4只能在約定日期(某月某日)的前11天出發,汽車1只能在約定日期的前12天出發.為了盡最大可能在各自允許的時間內將貨物運往城市乙,估計汽車4和汽車S應如何選擇各自的路徑.
某種產品按質量標準分成五個等級,等級編號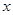 依次為1,2,3,4,5.現從一批產品中隨機抽取20件,對其等級編號進行統計分析,得到頻率分布表如下:
依次為1,2,3,4,5.現從一批產品中隨機抽取20件,對其等級編號進行統計分析,得到頻率分布表如下:
|
|
1 |
2 |
3 |
4 |
5 |
|
頻率 |
|
0.2 |
0.45 |
|
|
(I)若所抽取的20件產品中,等級編號為4的恰有3件,等級編號為5的恰有2件,求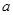 ,
,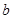 ,
,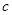 的值;
的值;
(Ⅱ)在(I)的條件下,將等級編號為4的3件產品記為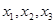 ,等級編號為5的2件產品記為
,等級編號為5的2件產品記為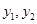 ,現從
,現從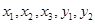 這5件產品中任取兩件(假定每件產品被取出的可能性相同),寫出所有可能的結果,并求這兩件產品的等級編號恰好相同的概率.
這5件產品中任取兩件(假定每件產品被取出的可能性相同),寫出所有可能的結果,并求這兩件產品的等級編號恰好相同的概率.
袋子中裝有大小形狀完全相同的m個紅球和n個白球,其中m,n滿足m>n≥2且m+n≤l0(m,n∈N+),若從中取出2個球,取出的2個球是同色的概率等于取出的2個球是異色的概率.
(Ⅰ) 求m,n的值;
(Ⅱ) 從袋子中任取3個球,設取到紅球的個數為 ,求
,求 的分布列與數學期望.
的分布列與數學期望.
【解析】第一問中利用 ,解得m=6,n=3.
,解得m=6,n=3.
第二問中, 的取值為0,1,2,3. P(
的取值為0,1,2,3. P( =0)=
=0)= 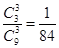 , P(
, P( =1)=
=1)= 
P( =2)=
=2)=  , P(
, P( =3)=
=3)= 
得到分布列和期望值
解:(I)據題意得到 解得m=6,n=3.
解得m=6,n=3.
(II) 的取值為0,1,2,3.
的取值為0,1,2,3.
P( =0)=
=0)= 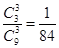 , P(
, P( =1)=
=1)= 
P( =2)=
=2)=  , P(
, P( =3)=
=3)= 
 的分布列為
的分布列為

所以E =2
=2
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com