日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

（08年唐山市二模）設，則函數的定義域為

     A．（1，2）      B．      C．      D．

設橢圓的左、右頂點分別為，點在橢圓上且異于兩點，為坐標原點.

（Ⅰ）若直線與的斜率之積為，求橢圓的離心率；

（Ⅱ）若，證明直線的斜率 滿足

【解析】(1)解：設點P的坐標為.由題意，有  ①

由，得，

由，可得，代入①并整理得

由于，故.于是，所以橢圓的離心率

（2）證明：（方法一）

依題意，直線OP的方程為，設點P的坐標為.

由條件得消去并整理得  ②

由，及，

得.

整理得.而，于是，代入②，

整理得

由，故，因此.

所以.

(方法二)

依題意，直線OP的方程為，設點P的坐標為.

由P在橢圓上，有

因為，，所以，即   ③

由，，得整理得.

于是，代入③，

整理得

解得，

所以.

（本小題滿分12分）已知二次函數滿足：，，且該函數的最小值為2.

⑴ 求此二次函數的解析式;

⑵ 若函數的定義域為= .(其中). 問是否存在這樣的兩個實數,使得函數的值域也為?若存在,求出的值;若不存在,請說明理由.

函數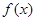的定義域為D，若存在閉區間[a，b]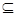D，使得函數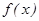滿足：

(1) 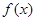在[a，b]內是單調函數；(2) 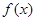在[a，b]上的值域為[2a，2b]，則稱區間[a，b]為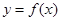的“和諧區間”．下列函數中存在“和諧區間”的是            (只需填符合題意的函數序號)

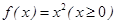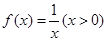①； ②； ③； ④．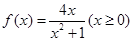

（08年潮州市二模理）（14分）已知函數的導數滿足，常數為方程的實數根．

⑴ 若函數的定義域為I，對任意，存在，使等式=成立，

 求證：方程不存在異于的實數根；

⑵ 求證：當時，總有成立；

⑶ 對任意，若滿足，求證．