
題目列表(包括答案和解析)
已知焦點在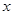 軸上的橢圓
軸上的橢圓 和雙曲線
和雙曲線 的離心率互為倒數,它們在第一象限交點的坐標為
的離心率互為倒數,它們在第一象限交點的坐標為 ,設直線
,設直線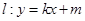 (其中
(其中 為整數).
為整數).
(1)試求橢圓 和雙曲線
和雙曲線 的標準方程;
的標準方程;
(2)若直線 與橢圓
與橢圓 交于不同兩點
交于不同兩點 ,與雙曲線
,與雙曲線 交于不同兩點
交于不同兩點 ,問是否存在直線
,問是否存在直線 ,使得向量
,使得向量 ,若存在,指出這樣的直線有多少條?若不存在,請說明理由.
,若存在,指出這樣的直線有多少條?若不存在,請說明理由.
已知焦點在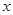 軸上的橢圓
軸上的橢圓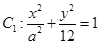 和雙曲線
和雙曲線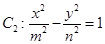 的離心率互為倒數,它們在第一象限交點的坐標為
的離心率互為倒數,它們在第一象限交點的坐標為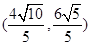 ,設直線
,設直線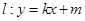 (其中
(其中 為整數).
為整數).
(1)試求橢圓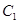 和雙曲線
和雙曲線 的標準方程;
的標準方程;
(2)若直線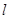 與橢圓
與橢圓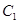 交于不同兩點
交于不同兩點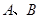 ,與雙曲線
,與雙曲線 交于不同兩點
交于不同兩點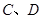 ,問是否存在直線
,問是否存在直線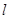 ,使得向量
,使得向量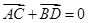 ,若存在,指出這樣的直線有多少條?若不存在,請說明理由.
,若存在,指出這樣的直線有多少條?若不存在,請說明理由.
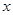 軸上的橢圓
軸上的橢圓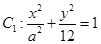 和雙曲線
和雙曲線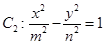 的離心率互為倒數,它們在第一象限交點的坐標為
的離心率互為倒數,它們在第一象限交點的坐標為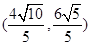 ,設直線
,設直線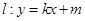 (其中
(其中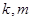 為整數).
為整數).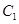 和雙曲線
和雙曲線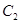 的標準方程;
的標準方程;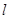 與橢圓
與橢圓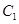 交于不同兩點
交于不同兩點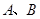 ,與雙曲線
,與雙曲線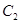 交于不同兩點
交于不同兩點 ,問是否存在直線
,問是否存在直線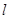 ,使得向量
,使得向量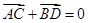 ,若存在,指出這樣的直線有多少條?若不存在,請說明理由.
,若存在,指出這樣的直線有多少條?若不存在,請說明理由. 的離心率為e,且b,e,
的離心率為e,且b,e, 為等比數列,曲線y=8-x2恰好過橢圓的焦點.
為等比數列,曲線y=8-x2恰好過橢圓的焦點. 的頂點和焦點分別是橢圓C1的焦點和頂點,設O為坐標原點,點A,B分別是C1和C2上的點,問是否存在A,B滿足
的頂點和焦點分別是橢圓C1的焦點和頂點,設O為坐標原點,點A,B分別是C1和C2上的點,問是否存在A,B滿足 .請說明理由.若存在,請求出直線AB的方程.
.請說明理由.若存在,請求出直線AB的方程.| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 3 |
| x2 |
| m2 |
| y2 |
| n2 |
| OA |
| 1 |
| 2 |
| OB |
一.1.B 2.B 3.A 4.B 5.A 6.D 7.C 8.A 9.A 10.C
二.11.5
12.36
13. 14.
14. 
15. 適合① ②
②
 的不等式如:
的不等式如: ,
,  或其它曲線型只要適合即可
或其它曲線型只要適合即可
三.16.解: (1)



∴ 即AB邊的長度為2.
…………… …………5分
即AB邊的長度為2.
…………… …………5分
(2)由已知及(1)有:

∴ ……………8分
……………8分
由正弦定理得:  ……………10分
……………10分
∴ =
= …………12分
…………12分
17.解: ①依題意可設 ………1分
………1分
則
對n=1,2,3,……都成立 ………3分

∴ 又 解得
解得

∴ ………6分
………6分
②∵
 …………9分
…………9分
∴ +
+  +
+ +…+
+…+
 ……12分
……12分
18.解:(Ⅰ)依題意,記“甲投一次命中”為事件A,“乙投一次命中”為事件B,
則 …………3分
…………3分
∵“甲、乙兩人各投球一次,都沒有命中”的事件為
 …………5分
…………5分
(Ⅱ)∵甲、乙兩人在罰球線各投球二次時,
甲命中1次,乙命中0次的概率為 …………7分
…………7分
甲命中2次,乙命中0次的概率為 …………9分
…………9分
甲命中2次,乙命中1次”的概率為 …………11分
…………11分
故甲、乙兩人在罰球線各投球兩次,甲投球命中的次數比乙投球命中的次數多的
概率為P= …………12分
…………12分
 19.解法1:取BE的中點O,連OC.
19.解法1:取BE的中點O,連OC.
∵BC=CE, ∴OC⊥BE.又AB⊥平面BCE.
以O為原點建立空間直角坐標系O-xyz如圖,
則由已知條件有: ,
, ,
,

 ,
, ……4分
……4分
設平面ADE的法向量為n= ,
,
則由n?



及n?



可取n
 ……6分
……6分
又AB⊥平面BCE. ∴AB⊥OC.OC⊥平面ABE
∴平面ABE的法向量可取為m= .
.
∵n?m
 ?
? =0,
=0,
∴n⊥m∴平面ADE⊥平面ABE. ……8分
⑵點C到平面ADE的距離為 ……12分
……12分
解法2:取BE的中點O,AE的中點F,連OC,OF,CD.則


 ∵AB⊥平面BCE,CD⊥平面BCE, AB=2CD
∵AB⊥平面BCE,CD⊥平面BCE, AB=2CD
∴CD 
 ,
,
 CD∴
CD∴ ∥ FD ……3分
∥ FD ……3分
∵BC=CE, ∴OC⊥BE.又AB⊥平面BCE.
∴OC⊥平面ABE. ∴FD⊥平面ABE.
從而平面ADE.⊥平面ABE. ……6分
②∵CD 
 ,延長AD, BC交于T
,延長AD, BC交于T
則C為BT的中點.
點C到平面ADE的距離等于點B到平面ADE的距離的 .……8分
.……8分
過B作BH⊥AE,垂足為H。∵平面ADE.⊥平面ABE。∴BH⊥平面BDE.
由已知有AB⊥BE.
BE= ,AB= 2, ∴BH=
,AB= 2, ∴BH= ,
,
從而點C到平面ADE的距離為 ……………… ……………12分
……………… ……………12分
或 ∥ FD, 點C到平面ADE的距離等于點O到平面ADE的距離為
∥ FD, 點C到平面ADE的距離等于點O到平面ADE的距離為 .
.
或取A B的中點M。易證 ∥ DA。點C到平面ADE的距離等于點M到平面ADE的距離為
∥ DA。點C到平面ADE的距離等于點M到平面ADE的距離為 .
.
20. 解:
(I)設O為原點,則
 =2
=2 ,
,
 =2
=2 。
。
而
 =
= ,得
,得 =
=
 ,
,
于是O、P、Q三點共線。 ……………2分
因為 所以PF∥QF/,且
所以PF∥QF/,且  ,……………3分
,……………3分
得



 ,
,
∴ ∴
∴ ……………5分
……………5分
因此橢圓的離心率為 雙曲線的離心率為
雙曲線的離心率為 ……………7分
……………7分
(II)設 、
、 ,
,
點P在雙曲線 的上,有
的上,有 。
。
則 .
.
所以 。 ①…………9分
。 ①…………9分
又由點Q在橢圓 上,有
上,有 。
。
同理可得 ②
……………10分
②
……………10分
∵O、P、Q三點共線。∴ 。
。
由①、②得 。
……………13分
。
……………13分
21. 解:(I)
 ……………1分
……………1分
由已知有: ∴
∴ ,∴
,∴ ……………3分
……………3分
從而

令 =0得:x1=1,x2=
=0得:x1=1,x2= . ∵
. ∵ ∴x2
∴x2
當x變化時, 、f(x)的變化情況如下表:
、f(x)的變化情況如下表:
x




+
-
+

增函數
減函數
增函數
從上表可知: 在
在 ,
, 上是增函數;
上是增函數;
在 ,上是減函數 ……………6分
,上是減函數 ……………6分
(II)∵m>0,∴m+1>1. 由(I)知:
①當0<m<1時, . 則最小值為
. 則最小值為 得:
得: ……8分
……8分
此時 .從而
.從而
∴最大值為 得
得
此時 適合. ……10分
適合. ……10分
②當m 1時,
1時,  在閉區間
在閉區間 上是增函數.
上是增函數.
∴最小值為
 ⑴
⑴
最大值為
 =0. ⑵………12分
=0. ⑵………12分
由⑵得: ⑶
⑶
⑶代入⑴得: .即
.即
又m 1,
1,  ∴
∴ 從而
從而
∴此時的a,m不存在
綜上知:
 ,
, .
………14分
.
………14分
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com