
��֪���c(di��n)��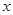 �S�ϵęE�A
�S�ϵęE�A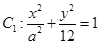 ���p����
���p����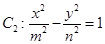 ���x���ʻ��鵹��(sh��)������?c��)ڵ�һ�����c(di��n)������(bi��o)��
���x���ʻ��鵹��(sh��)������?c��)ڵ�һ�����c(di��n)������(bi��o)��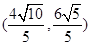 ���O(sh��)ֱ��
���O(sh��)ֱ��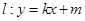 ������
������ ������(sh��)��.
������(sh��)��.
��1��ԇ��E�A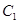 ���p����
���p���� �Ę�(bi��o)��(zh��n)���̣�
�Ę�(bi��o)��(zh��n)���̣�
��2����ֱ��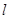 �c�E�A
�c�E�A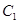 ���ڲ�ͬ���c(di��n)
���ڲ�ͬ���c(di��n)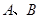 ���c�p����
���c�p���� ���ڲ�ͬ���c(di��n)
���ڲ�ͬ���c(di��n)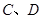 ����(w��n)�Ƿ����ֱ��
����(w��n)�Ƿ����ֱ��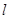 ��ʹ������
��ʹ������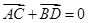 �������ڣ�ָ���@�ӵ�ֱ���ж��ٗl���������ڣ�Ո(q��ng)�f(shu��)������.
�������ڣ�ָ���@�ӵ�ֱ���ж��ٗl���������ڣ�Ո(q��ng)�f(shu��)������.
��1���E�A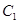 �飺
�飺 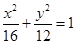 ���p����
���p���� �飺
�飺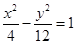 ��2�����ڣ��M��l����ֱ������9�l.
��2�����ڣ��M��l����ֱ������9�l.
����ԇ�}��������1�����c(di��n)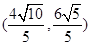 ����
����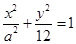 ��������E�A
��������E�A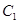 �ķ��̣�ͨ�^(gu��)�E�A
�ķ��̣�ͨ�^(gu��)�E�A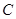 ���x��������p����
���x��������p���� ���x���ʣ�(li��n)���x���ʺ��p�����ķ��̣����
���x���ʣ�(li��n)���x���ʺ��p�����ķ��̣����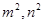 ����2����?y��n)�ֱ��
����2����?y��n)�ֱ��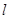 �c�E�A
�c�E�A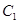 ���ڲ�ͬ���c(di��n)
���ڲ�ͬ���c(di��n)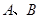 ������(li��n)��ֱ���͙E�A���̣���ȥ
������(li��n)��ֱ���͙E�A���̣���ȥ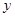 ���������̼���.
���������̼���.
ԇ�}��������1�����c(di��n)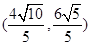 ����
����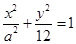 ���
���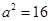
���E�A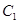 �飺
�飺 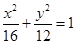 �� ��2�֣�
�� ��2�֣�
�E�A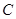 ���x���ʞ�
���x���ʞ�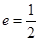 ���p����
���p���� ���x���ʞ�
���x���ʞ�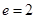 �� ��3�֣�
�� ��3�֣�
��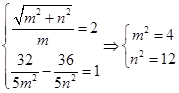 ��
��
���p���� �飺
�飺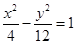 ��6�֣�
��6�֣�
��2����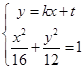 ��ȥ
��ȥ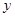 ����(ji��n)�����ã�
����(ji��n)�����ã�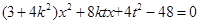
�O(sh��)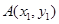 ��
��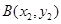 ���t
���t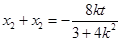
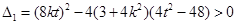 �� ��8�֣�
�� ��8�֣�
��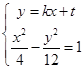 ��ȥ
��ȥ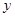 ����(ji��n)�����ã�
����(ji��n)�����ã�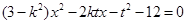
�O(sh��)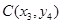 ��
��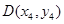 ���t
���t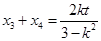
 �� ��10�֣�
�� ��10�֣�
��?y��n)?img src="http://thumb.zyjl.cn/pic5/tikupic/a1/b/c9pzd.png" style="vertical-align:middle;" />������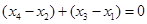 ��
��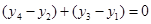
��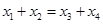 �ã�
�ã�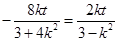 ��
��
����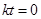 ��
��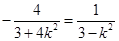 ������ʽ���
������ʽ���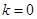 ��
��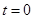 ��
��
��(d��ng)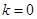 �r(sh��)���ɢٺ͢ڵ�
�r(sh��)���ɢٺ͢ڵ�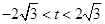 ����
����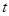 ������(sh��)��
������(sh��)��
����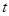 ��ֵ��
��ֵ��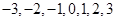
��(d��ng)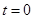 ���ɢٺ͢ڵ�
���ɢٺ͢ڵ�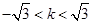 ����
����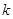 ������(sh��)������
������(sh��)������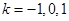 ��
��
���ǝM��l����ֱ������9�l�� ��13�֣�
���c(di��n)��1.��E�A���p�����ķ���.



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��ƽ��ֱ������(bi��o)ϵ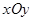 �У���֪�E�A
�У���֪�E�A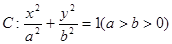 �����c(di��n)��
�����c(di��n)�� ���ҙE�A
���ҙE�A ���x����
���x����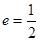 .
.
(1)��E�A �ķ��̣�
�ķ��̣�
(2)�O(sh��)�E�A ��������c(di��n)�քe��
��������c(di��n)�քe��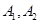 ,
,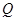 �ǙE�A
�ǙE�A �Ϯ���
�Ϯ���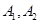 ����һ�c(di��n),ֱ��
����һ�c(di��n),ֱ��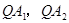 �քe��
�քe��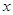 �S���c(di��n)
�S���c(di��n)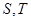 ,�C��:
,�C��: �鶨ֵ,�����ԓ��ֵ��
�鶨ֵ,�����ԓ��ֵ��
(3)�ڙE�A �ϣ��Ƿ�����c(di��n)
�ϣ��Ƿ�����c(di��n)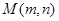 ��ʹ��ֱ��
��ʹ��ֱ��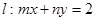 �c�A
�c�A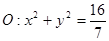 �ཻ�ڲ�ͬ�ă��c(di��n)
�ཻ�ڲ�ͬ�ă��c(di��n)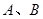 ����
����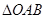 ����e��������ڣ�����c(di��n)
����e��������ڣ�����c(di��n)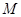 ������(bi��o)����(du��)��(y��ng)��
������(bi��o)����(du��)��(y��ng)��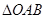 ����e���������ڣ�Ո(q��ng)�f(shu��)������.
����e���������ڣ�Ո(q��ng)�f(shu��)������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
�o���E�A ��
��
 ���Q�A����ԭ�c(di��n)
���Q�A����ԭ�c(di��n) ���돽��
���돽�� �ĈA�ǙE�A
�ĈA�ǙE�A �ġ���(zh��n)�A�������E�A
�ġ���(zh��n)�A�������E�A ��һ��(g��)���c(di��n)��
��һ��(g��)���c(di��n)�� ��������S�ϵ�һ��(g��)���c(di��n)��
��������S�ϵ�һ��(g��)���c(di��n)�� �ľ��x��
�ľ��x�� .
.
(��)��E�A �ķ��̺��䡰��(zh��n)�A�����̣�
�ķ��̺��䡰��(zh��n)�A�����̣�
(��)�c(di��n) �ǙE�A
�ǙE�A �ġ���(zh��n)�A���ϵ�һ��(g��)��(d��ng)�c(di��n)���^(gu��)��(d��ng)�c(di��n)
�ġ���(zh��n)�A���ϵ�һ��(g��)��(d��ng)�c(di��n)���^(gu��)��(d��ng)�c(di��n) ��ֱ��
��ֱ�� ��ʹ��
��ʹ�� �c�E�A
�c�E�A ��ֻ��һ��(g��)���c(di��n)��ԇ�Д�
��ֻ��һ��(g��)���c(di��n)��ԇ�Д� �Ƿ�ֱ�����f(shu��)�����ɣ�
�Ƿ�ֱ�����f(shu��)�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪�E�A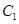 �����タ
�����タ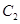 �Ľ��c(di��n)����
�Ľ��c(di��n)���� �S�ϣ�
�S�ϣ�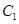 �����ĺ�
�����ĺ�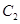 ����c(di��n)����ԭ�c(di��n)
����c(di��n)����ԭ�c(di��n) ��ÿ�l������ȡ�ɂ�(g��)�c(di��n)����������(bi��o)ӛ��ڱ��У�
��ÿ�l������ȡ�ɂ�(g��)�c(di��n)����������(bi��o)ӛ��ڱ��У�
 |  | 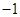 | 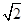 | 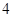 |
 | 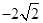 | 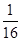 | 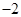 | 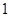 |
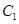 ��
��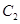 �Ę�(bi��o)��(zh��n)���̣�
�Ę�(bi��o)��(zh��n)���̣�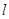 �c
�c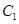 ����ֻ��һ��(g��)�����c(di��n)
����ֻ��һ��(g��)�����c(di��n) �����c
�����c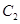 �Ĝ�(zh��n)������
�Ĝ�(zh��n)������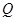 ��ԇ̽����������(bi��o)ƽ���(n��i)�Ƿ���ڶ��c(di��n)
��ԇ̽����������(bi��o)ƽ���(n��i)�Ƿ���ڶ��c(di��n)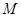 ��ʹ����
��ʹ����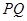 ��ֱ���ĈA���^(gu��)�c(di��n)
��ֱ���ĈA���^(gu��)�c(di��n)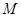 �������ڣ����
�������ڣ����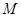 �c(di��n)������(bi��o)���������ڣ�Ո(q��ng)�f(shu��)������.
�c(di��n)������(bi��o)���������ڣ�Ո(q��ng)�f(shu��)������.�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪ ��
�� �ǙE�A
�ǙE�A
 �����ҽ��c(di��n)�����x����
�����ҽ��c(di��n)�����x���� ���c(di��n)
���c(di��n) ��E�A�ϵ�һ��(g��)��(d��ng)�c(di��n)��
��E�A�ϵ�һ��(g��)��(d��ng)�c(di��n)�� �ă�(n��i)�ЈA��e�����ֵ��
�ă�(n��i)�ЈA��e�����ֵ�� .
.
(1) ��E�A�ķ��̣�
(2) �� �ǙE�A�ϲ��غϵ��Ă�(g��)�c(di��n)���M������
�ǙE�A�ϲ��غϵ��Ă�(g��)�c(di��n)���M������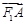 �c
�c ������
������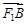 �c
�c ��
��
������ ����
���� ��ȡֵ����.
��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪�E�A ��������ԭ�c(di��n)�����c(di��n)��
��������ԭ�c(di��n)�����c(di��n)��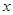 �S�ϣ��x����
�S�ϣ��x����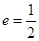 ������һ��(g��)��c(di��n)ǡ���ǒ��タ
������һ��(g��)��c(di��n)ǡ���ǒ��タ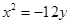 �Ľ��c(di��n).
�Ľ��c(di��n).
������E�A �ķ��̣�
�ķ��̣�
�����O(sh��)�E�A �c����
�c����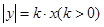 �Ľ��c(di��n)��
�Ľ��c(di��n)��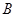 ��
�� ����
����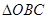 ��e�����ֵ.
��e�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
���p�����c�E�A ����ͬ�Ľ��c(di��n)���c�p����
����ͬ�Ľ��c(di��n)���c�p���� ����ͬ�u���������p��������.
����ͬ�u���������p��������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��D����֪�E�A ��
�� ���L(zh��ng)�S�����Ҷ��c(di��n)����(d��ng)�c(di��n)
���L(zh��ng)�S�����Ҷ��c(di��n)����(d��ng)�c(di��n) �M��
�M�� ��(li��n)�Y(ji��)
��(li��n)�Y(ji��) �����E�A���c(di��n)
�����E�A���c(di��n) ��
�� 
��1����(d��ng) ��
�� �r(sh��)���O(sh��)
�r(sh��)���O(sh��) ����
����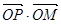 ��ֵ��
��ֵ��
��2����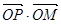 �鳣��(sh��)��̽��
�鳣��(sh��)��̽�� �M��ėl�������f(shu��)�����ɣ�
�M��ėl�������f(shu��)�����ɣ�
��3��ֱ�ӌ�(xi��)��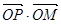 �鳣��(sh��)��һ��(g��)��ͬ�ڣ�2���Y(ji��)Փ��͵ĎΗl����
�鳣��(sh��)��һ��(g��)��ͬ�ڣ�2���Y(ji��)Փ��͵ĎΗl����
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��ֱ������(bi��o)ϵ �У�ֱ��
�У�ֱ�� �ķ��̞�
�ķ��̞� ������
������ �ą���(sh��)���̞�
�ą���(sh��)���̞� ��
�� �酢��(sh��)��.
�酢��(sh��)��.
��I����֪�ژO����(bi��o)���cֱ������(bi��o)ϵ ȡ��ͬ���L(zh��ng)�Ȇ�λ������ԭ�c(di��n)
ȡ��ͬ���L(zh��ng)�Ȇ�λ������ԭ�c(di��n) ��O�c(di��n)����
��O�c(di��n)���� �S�����S��O�S�����c(di��n)
�S�����S��O�S���У��c(di��n) �ĘO����(bi��o)�飨4��
�ĘO����(bi��o)�飨4�� �����Д��c(di��n)
�����Д��c(di��n) �cֱ��
�cֱ�� ��λ���P(gu��n)ϵ��
��λ���P(gu��n)ϵ��
��II���O(sh��)�c(di��n) ������
������ �ϵ�һ��(g��)��(d��ng)�c(di��n)��������ֱ��
�ϵ�һ��(g��)��(d��ng)�c(di��n)��������ֱ�� �ľ��x����Сֵ.
�ľ��x����Сֵ.
�鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com