
題目列表(包括答案和解析)
如圖,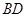 為⊙
為⊙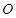 的直徑,
的直徑,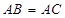 ,
,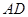 交
交 于點
于點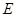 ,
,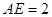 ,
,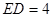 .
.
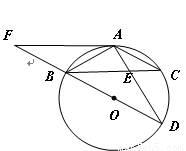
(1)求證: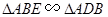 ;
;
(2)求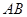 的長;
的長;
(3)延長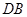 到
到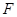 ,使得
,使得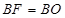 ,連接
,連接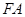 ,試判斷直
線
,試判斷直
線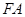 與⊙
與⊙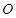 的位置關系,并說明理由.
的位置關系,并說明理由.
【解析】(1)根據AB=AC,可得∠ABC=∠C,利用等量代換可得∠ABC=∠D然后即可證明△ABE∽△ADB.
(2)根據△ABE∽△ADB,利用其對應邊成比例,將已知數值代入即可求得AB的長.
(3)連接OA,根據BD為⊙O的直徑可得∠BAD=90°,利用勾股定理求得BD,然后再求證∠OAF=90°即可
(本題滿分8分)已知![]() 在平面直角坐標系中的位置如下圖所示.(1)分別寫出圖中點
在平面直角坐標系中的位置如下圖所示.(1)分別寫出圖中點![]() 的坐標;(2)畫出
的坐標;(2)畫出![]() 繞點
繞點![]() 按逆時針方向旋轉
按逆時針方向旋轉![]() 后的
后的![]() ;(3)求點
;(3)求點![]() 旋轉到點
旋轉到點![]() 所經過的路線長(結果保留
所經過的路線長(結果保留![]() ).
).
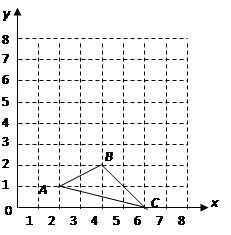
【解析】(1)在直角坐標系中讀出A的坐標,點C的坐標;
(2)根據旋轉的性質畫出△ABC繞點A按逆時針方向旋轉90°后的△A′B′C′;
(3)先根據勾股定理求出AC的長,然后利用弧長的計算公式求解即可
如圖,在梯形ABCD中,AD∥BC,∠D=90°,BE⊥AC,E為垂足, AC=BC.
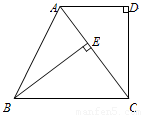
⑴求證:CD=BE.⑵若AD=3,DC=4,求AE.
【解析】(1)根據平行線的性質可以得到∠DAC=∠BCE,再根據已知就可以證明△BCE≌△CAD,然后根據其對應邊相等就可以得到;
(2)首先根據勾股定理的AC的長,再根據(1)的結論就可以求出AE
如圖,在梯形ABCD中,AD∥BC,∠D=90°,BE⊥AC,E為垂足, AC=BC.
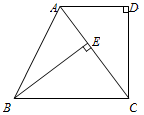
⑴求證:CD=BE.⑵若AD=3,DC=4,求AE.
【解析】(1)根據平行線的性質可以得到∠DAC=∠BCE,再根據已知就可以證明△BCE≌△CAD,然后根據其對應邊相等就可以得到;
(2)首先根據勾股定理的AC的長,再根據(1)的結論就可以求出AE
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com