
題目列表(包括答案和解析)
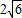 ,則該棱柱的外接球的表面積為 .
,則該棱柱的外接球的表面積為 . ,則該棱柱的外接球的表面積為_(kāi)_______.
,則該棱柱的外接球的表面積為_(kāi)_______.若正三棱柱的底面邊長(zhǎng)為3,側(cè)棱長(zhǎng)為![]() ,則該棱柱的外接球的表面積為_(kāi)_______.
,則該棱柱的外接球的表面積為_(kāi)_______.
正三棱柱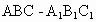 的底面邊長(zhǎng)為a,側(cè)棱長(zhǎng)為
的底面邊長(zhǎng)為a,側(cè)棱長(zhǎng)為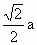 ,若經(jīng)過(guò)對(duì)角線
,若經(jīng)過(guò)對(duì)角線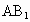 且與對(duì)角線
且與對(duì)角線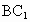 平行的平面交上底面于
平行的平面交上底面于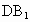 .(1)試確定D點(diǎn)的位置,并證明你的結(jié)論;(2)求證:平面
.(1)試確定D點(diǎn)的位置,并證明你的結(jié)論;(2)求證:平面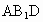 ⊥平面
⊥平面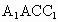 ;(3)求二面角
;(3)求二面角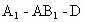 的大小.
的大小.
如圖,正三棱柱![]() 的底面邊長(zhǎng)為
的底面邊長(zhǎng)為![]() ,側(cè)棱長(zhǎng)為
,側(cè)棱長(zhǎng)為![]() ,點(diǎn)
,點(diǎn)![]() 在棱
在棱![]() 上.
上.
(1) 若![]() ,求證:直線
,求證:直線![]() 平面
平面![]() ;
;
(2)是否存在點(diǎn)![]() , 使平面
, 使平面![]() ⊥平面
⊥平面![]() ,若存在,請(qǐng)確定點(diǎn)
,若存在,請(qǐng)確定點(diǎn)![]() 的位置,若不存在,請(qǐng)說(shuō)明理由;
的位置,若不存在,請(qǐng)說(shuō)明理由;
(3)請(qǐng)指出點(diǎn)![]() 的位置,使二面角
的位置,使二面角![]() 平面角的大小為
平面角的大小為![]() .
.
一.1.B 2.B 3.A 4.B 5.A 6.D 7.C 8.A 9.A 10.C
二.11.5
12.36
13. 14.
14. 
15. 適合① ②
②
 的不等式如:
的不等式如: ,
,  或其它曲線型只要適合即可
或其它曲線型只要適合即可
三.16.解: (1)



∴ 即AB邊的長(zhǎng)度為2.
…………… …………5分
即AB邊的長(zhǎng)度為2.
…………… …………5分
(2)由已知及(1)有:

∴ ……………8分
……………8分
由正弦定理得:  ……………10分
……………10分
∴ =
= …………12分
…………12分
17.解: ①依題意可設(shè) ………1分
………1分
則
對(duì)n=1,2,3,……都成立 ………3分

∴ 又 解得
解得

∴ ………6分
………6分
②∵
 …………9分
…………9分
∴ +
+  +
+ +…+
+…+
 ……12分
……12分
18.解:(Ⅰ)依題意,記“甲投一次命中”為事件A,“乙投一次命中”為事件B,
則 …………3分
…………3分
∵“甲、乙兩人各投球一次,都沒(méi)有命中”的事件為
 …………5分
…………5分
(Ⅱ)∵甲、乙兩人在罰球線各投球二次時(shí),
甲命中1次,乙命中0次的概率為 …………7分
…………7分
甲命中2次,乙命中0次的概率為 …………9分
…………9分
甲命中2次,乙命中1次”的概率為 …………11分
…………11分
故甲、乙兩人在罰球線各投球兩次,甲投球命中的次數(shù)比乙投球命中的次數(shù)多的
概率為P= …………12分
…………12分
 19.解法1:取BE的中點(diǎn)O,連OC.
19.解法1:取BE的中點(diǎn)O,連OC.
∵BC=CE, ∴OC⊥BE.又AB⊥平面BCE.
以O(shè)為原點(diǎn)建立空間直角坐標(biāo)系O-xyz如圖,
則由已知條件有: ,
, ,
,

 ,
, ……4分
……4分
設(shè)平面ADE的法向量為n= ,
,
則由n?



及n?



可取n
 ……6分
……6分
又AB⊥平面BCE. ∴AB⊥OC.OC⊥平面ABE
∴平面ABE的法向量可取為m= .
.
∵n?m
 ?
? =0,
=0,
∴n⊥m∴平面ADE⊥平面ABE. ……8分
⑵點(diǎn)C到平面ADE的距離為 ……12分
……12分
解法2:取BE的中點(diǎn)O,AE的中點(diǎn)F,連OC,OF,CD.則


 ∵AB⊥平面BCE,CD⊥平面BCE, AB=2CD
∵AB⊥平面BCE,CD⊥平面BCE, AB=2CD
∴CD 
 ,
,
 CD∴
CD∴ ∥ FD ……3分
∥ FD ……3分
∵BC=CE, ∴OC⊥BE.又AB⊥平面BCE.
∴OC⊥平面ABE. ∴FD⊥平面ABE.
從而平面ADE.⊥平面ABE. ……6分
②∵CD 
 ,延長(zhǎng)AD, BC交于T
,延長(zhǎng)AD, BC交于T
則C為BT的中點(diǎn).
點(diǎn)C到平面ADE的距離等于點(diǎn)B到平面ADE的距離的 .……8分
.……8分
過(guò)B作BH⊥AE,垂足為H。∵平面ADE.⊥平面ABE。∴BH⊥平面BDE.
由已知有AB⊥BE.
BE= ,AB= 2, ∴BH=
,AB= 2, ∴BH= ,
,
從而點(diǎn)C到平面ADE的距離為 ……………… ……………12分
……………… ……………12分
或 ∥ FD, 點(diǎn)C到平面ADE的距離等于點(diǎn)O到平面ADE的距離為
∥ FD, 點(diǎn)C到平面ADE的距離等于點(diǎn)O到平面ADE的距離為 .
.
或取A B的中點(diǎn)M。易證 ∥ DA。點(diǎn)C到平面ADE的距離等于點(diǎn)M到平面ADE的距離為
∥ DA。點(diǎn)C到平面ADE的距離等于點(diǎn)M到平面ADE的距離為 .
.
20. 解:
(I)設(shè)O為原點(diǎn),則
 =2
=2 ,
,
 =2
=2 。
。
而
 =
= ,得
,得 =
=
 ,
,
于是O、P、Q三點(diǎn)共線。 ……………2分
因?yàn)?sub> 所以PF∥QF/,且
所以PF∥QF/,且  ,……………3分
,……………3分
得



 ,
,
∴ ∴
∴ ……………5分
……………5分
因此橢圓的離心率為 雙曲線的離心率為
雙曲線的離心率為 ……………7分
……………7分
(II)設(shè) 、
、 ,
,
點(diǎn)P在雙曲線 的上,有
的上,有 。
。
則 .
.
所以 。 ①…………9分
。 ①…………9分
又由點(diǎn)Q在橢圓 上,有
上,有 。
。
同理可得 ②
……………10分
②
……………10分
∵O、P、Q三點(diǎn)共線。∴ 。
。
由①、②得 。
……………13分
。
……………13分
21. 解:(I)
 ……………1分
……………1分
由已知有: ∴
∴ ,∴
,∴ ……………3分
……………3分
從而

令 =0得:x1=1,x2=
=0得:x1=1,x2= . ∵
. ∵ ∴x2
∴x2
當(dāng)x變化時(shí), 、f(x)的變化情況如下表:
、f(x)的變化情況如下表:
x




+
-
+

增函數(shù)
減函數(shù)
增函數(shù)
從上表可知: 在
在 ,
, 上是增函數(shù);
上是增函數(shù);
在 ,上是減函數(shù) ……………6分
,上是減函數(shù) ……………6分
(II)∵m>0,∴m+1>1. 由(I)知:
①當(dāng)0<m<1時(shí), . 則最小值為
. 則最小值為 得:
得: ……8分
……8分
此時(shí) .從而
.從而
∴最大值為 得
得
此時(shí) 適合. ……10分
適合. ……10分
②當(dāng)m 1時(shí),
1時(shí),  在閉區(qū)間
在閉區(qū)間 上是增函數(shù).
上是增函數(shù).
∴最小值為
 ⑴
⑴
最大值為
 =0. ⑵………12分
=0. ⑵………12分
由⑵得: ⑶
⑶
⑶代入⑴得: .即
.即
又m 1,
1,  ∴
∴ 從而
從而
∴此時(shí)的a,m不存在
綜上知:
 ,
, .
………14分
.
………14分
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com