題目列表(包括答案和解析)
如圖1，在Rt△ABC中，∠C=90°，BC=3，AC=6，D，E分別是AC，AB上的點，且DE∥BC，DE=2，將△ADE沿DE折起到△A1DE的位置，使A1C⊥CD,如圖2.
（1） 求證：A1C⊥平面BCDE；
（2） 若M是A1D的中點，求CM與平面A1BE所成角的大小；
（3） 線段BC上是否存在點P，使平面A1DP與平面A1BE垂直？說明理由
【解析】（1）∵
DE∥BC∴
∴
∴
∴
又∵
∴
（2）如圖，以C為坐標原點，建立空間直角坐標系C-xyz，
則
設平面
的法向量為
，則
,又
，
，所以
，令
，則
，所以
，
設CM與平面所成角為
。因為
，
所以
所以CM與平面所成角為
。
完成下列反證法證題的全過程：已知0＜a≤3，函數f(x)＝x3－ax在區間[1，＋∞)上是增函數，設當x0≥1，f(x0)≥1時，有f(f(x0))＝x0，求證：f(x0)＝x0．
證明：假設f(x0)≠x0，則必有 ① 或 ② ．
若 ③ ，由f(x)在區間[1，＋∞)上是增函數，則f(f(x0))＞f(x0)．
又f(f(x0))＝x0，所以f(x0)＜x0，這與 ④ 矛盾．
若x0＞f(x0)≥1，由f(x)在區間[1，＋∞)上是增函數，則 ⑤ ．
又f(f(x0))＝x0，所以f(x0)＞x0，這與 ⑥ 矛盾．
綜上所述，當x0≥1，f(x0)≥1且f(f(x0))＝x0時，有f(x0)＝x0．
完成下列反證法證題的全過程：
已知0＜a≤3，函數f(x)＝x3－ax在區間[1，＋∞)上是增函數，設當x0≥1，f(x0)≥1時，有f(f(x0))＝x0，求證：f(x0)＝x0．
證明：假設f(x0)≠x0，則必有 ① 或 ② ．
若 ③ ，由f(x)在區間[1，＋∞)上是增函數，則f(f(x0))＞f(x0)．
又f(f(x0))＝x0，所以f(x0)＜x0，這與 ④ 矛盾．
若x0＞f(x0)≥1，由f(x)在區間[1，＋∞)上是增函數，則 ⑤ ．
又f(f(x0))＝x0，所以f(x0)＞x0，這與 ⑥ 矛盾．
綜上所述，當x0≥1，f(x0)≥1且f(f(x0))＝x0時，有f(x0)＝x0．
| 2 |
| 2 |
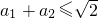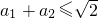．”．湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com