
題目列表(包括答案和解析)
(本小題滿分12分)袋中裝有黑球和白球共7個,從中任取2個球都是白球的概率為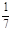 .現有甲、乙兩人從袋中輪流摸取1個球,甲先取,乙后取,然后甲再取,
.現有甲、乙兩人從袋中輪流摸取1個球,甲先取,乙后取,然后甲再取,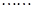 ,取后不放回,直到兩人中有一人取到白球時即終止,每個球在每一次被取出的機會是等可能的.求:
,取后不放回,直到兩人中有一人取到白球時即終止,每個球在每一次被取出的機會是等可能的.求:
(1)則袋中原有白球的個數;
(2)取球2次終止的概率;
(3)甲取到白球的概率
(本小題滿分12分)袋中裝有黑球和白球共7個,從中任取2個球都是白球的概率為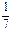 .現有甲、乙兩人從袋中輪流摸取1個球,甲先取,乙后取,然后甲再取,
.現有甲、乙兩人從袋中輪流摸取1個球,甲先取,乙后取,然后甲再取,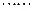 ,取后不放回,直到兩人中有一人取到白球時即終止,每個球在每一次被取出的機會是等可能的.求:
,取后不放回,直到兩人中有一人取到白球時即終止,每個球在每一次被取出的機會是等可能的.求:
(1)則袋中原有白球的個數;
(2)取球2次終止的概率;
(3)甲取到白球的概率
 .現有甲、乙兩人從袋中輪流摸取1個球,甲先取,乙后取,然后甲再取,
.現有甲、乙兩人從袋中輪流摸取1個球,甲先取,乙后取,然后甲再取, ,取后不放回,直到兩人中有一人取到白球時即終止,每個球在每一次被取出的機會是等可能的.求:
,取后不放回,直到兩人中有一人取到白球時即終止,每個球在每一次被取出的機會是等可能的.求: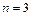 ,求取到的4個球全是紅球的概率;
,求取到的4個球全是紅球的概率;

 ,求n的值.
,求n的值.(本小題滿分12分)袋中裝有黑球和白球共7個,從中任取2個球都是白球的概率為![]() 現有甲、乙兩人從袋中輪流摸取1球,甲先取,乙后取,然后甲再取……取后不放回,直到兩人中有一人取到白球時既終止,每個球在每一次被取出的機會是等可能的,用
現有甲、乙兩人從袋中輪流摸取1球,甲先取,乙后取,然后甲再取……取后不放回,直到兩人中有一人取到白球時既終止,每個球在每一次被取出的機會是等可能的,用![]() 表示取球終止所需要的取球次數.
表示取球終止所需要的取球次數.
(Ⅰ)求袋中原有的白球的個數;
(Ⅱ)求甲取到白球的概率.
一、選擇題:(每小題5分,共50分)
題號
1
2
3
4
5
6
7
8
9
10
答案
B
D
B
A
C
C
C
A
A
B
二、填空題:(每小題4分,共24分)
11.文科數學.files/image222.gif) 12.4 13.
12.4 13.文科數學.files/image224.gif) 14.
14.文科數學.files/image226.gif) 15.4 16.
15.4 16.文科數學.files/image228.gif)
三、解答題:(共76分,以下各題為累計得分,其他解答請相應給分)
17.解:(I)文科數學.files/image230.gif)
文科數學.files/image232.gif)
文科數學.files/image234.gif)
由文科數學.files/image236.gif) ,得
,得文科數學.files/image238.gif) 。
。
又當文科數學.files/image240.gif) 時
時文科數學.files/image242.gif) ,得
,得文科數學.files/image244.gif)
文科數學.files/image246.gif)
(Ⅱ)當文科數學.files/image248.gif)
即文科數學.files/image250.gif) 時函數遞增。
時函數遞增。
故文科數學.files/image097.gif) 的單調增區間為
的單調增區間為文科數學.files/image253.gif) ,
,文科數學.files/image255.gif)
18.解:(I)各取1個球的結果有(紅,紅1)(紅,紅2)(紅,白1)(紅,白2)(紅,黑)
(白,紅2)(白,紅2)(白,白1)(白,白2)(白,黑)(白,紅1)(白,紅2)
(白,白1)(白,白2)(白,黑)(黑1,紅1)(黑1,紅2)(黑1,白1)(黑1,白2)(黑1,黑)(黑2,紅1)(黑2,紅2)(黑2,白1)(黑2,白2)(黑2,黑)(黑3,紅1)
(黑3,紅2)(黑3,白1)(黑3,白2)(黑3,黑)
等30種情況
其中恰有1白1黑有(白,黑)…(黑3,白2)8種情況,
故1白1黑的概率為文科數學.files/image257.gif)
(Ⅱ)2紅有2種,2白有4種,2黑有3種,
故兩球顏色相同的概率為文科數學.files/image259.gif)
(Ⅲ)1紅有1×3+2×5=13(種),2紅有2種,
故至少有1個紅球的概率為文科數學.files/image261.gif)
19.解:(I)側視圖文科數學.files/image263.jpg) (高4,底2
(高4,底2文科數學.files/image265.gif) )
)
文科數學.files/image267.gif)
(Ⅱ)證明,由文科數學.files/image162.gif) 面ABC得
面ABC得文科數學.files/image162.gif) AC,又由俯視圖知AB
AC,又由俯視圖知AB文科數學.files/image271.gif) AC,
AC,文科數學.files/image273.gif) ,
,
文科數學.files/image275.gif) 面PAB
面PAB
又AC文科數學.files/image277.gif) 面PAC,
面PAC,文科數學.files/image279.gif) 面PAC
面PAC文科數學.files/image271.gif) 面PAB
面PAB
(Ⅲ)文科數學.files/image282.gif) 面ABC,
面ABC,文科數學.files/image284.gif) 為直線PC與底面ABC所成的角
為直線PC與底面ABC所成的角
在文科數學.files/image286.gif) 中,PA=4,AC=
中,PA=4,AC=文科數學.files/image288.gif) ,
,文科數學.files/image290.gif) ,
,
文科數學.files/image292.gif)
20.解:(I)由題意設C的方程為文科數學.files/image294.gif) 由
由文科數學.files/image296.gif) ,得
,得文科數學.files/image298.gif) 。
。
文科數學.files/image300.gif)
設直線文科數學.files/image178.gif) 的方程為
的方程為文科數學.files/image303.gif) ,由
,由文科數學.files/image305.gif)
②代入①化簡整理得 文科數學.files/image307.gif)
因直線文科數學.files/image178.gif) 與拋物線C相交于不同的兩點,
與拋物線C相交于不同的兩點,
故文科數學.files/image310.gif)
即文科數學.files/image312.gif) ,解得
,解得文科數學.files/image314.gif) 又
又文科數學.files/image316.gif) 時僅交一點,
時僅交一點,文科數學.files/image318.gif)
(Ⅱ)設文科數學.files/image320.gif) ,由由(I)知
,由由(I)知
文科數學.files/image322.gif)
文科數學.files/image324.gif)
文科數學.files/image326.gif)
21.解:(I)文科數學.files/image328.gif) 由
由文科數學.files/image330.gif) 得
得文科數學.files/image332.gif)
于是文科數學.files/image334.gif) 故
故文科數學.files/image336.gif)
文科數學.files/image279.gif) 切線方程為
切線方程為文科數學.files/image339.gif) ,即
,即文科數學.files/image341.gif)
(Ⅱ)令文科數學.files/image343.gif) ,解得
,解得文科數學.files/image345.gif)
①當文科數學.files/image347.gif) 時,即
時,即文科數學.files/image349.gif) 時,在
時,在文科數學.files/image351.gif) 內,
內,文科數學.files/image353.gif) ,于是
,于是文科數學.files/image097.gif) 在[1,4]內為增函數。從而
在[1,4]內為增函數。從而文科數學.files/image356.gif)
②當文科數學.files/image358.gif) ,即
,即文科數學.files/image360.gif) ,在
,在文科數學.files/image362.gif) 內,
內,文科數學.files/image364.gif) ,于是
,于是文科數學.files/image097.gif) 在[1,4]內為減函數,從而
在[1,4]內為減函數,從而文科數學.files/image367.gif)
③當文科數學.files/image369.gif) 時,
時,文科數學.files/image097.gif) 在
在文科數學.files/image372.gif) 內遞減,在
內遞減,在文科數學.files/image374.gif) 內遞增,故
內遞增,故文科數學.files/image097.gif) 在[1,4]上的最大值為
在[1,4]上的最大值為文科數學.files/image377.gif) 與
與文科數學.files/image379.gif) 的較大者。
的較大者。
由文科數學.files/image381.gif) ,得
,得文科數學.files/image383.gif) ,故當
,故當文科數學.files/image385.gif) 時,
時,文科數學.files/image387.gif)
當文科數學.files/image389.gif) 時,
時,文科數學.files/image367.gif)
22.解:(I)設文科數學.files/image197.gif) 的首項為
的首項為文科數學.files/image393.gif) ,公差為d,于是由
,公差為d,于是由文科數學.files/image395.gif)
解得文科數學.files/image397.gif)
文科數學.files/image399.gif)
(Ⅱ)文科數學.files/image401.gif)
由文科數學.files/image403.gif) ①
①
得文科數學.files/image405.gif) ②
②
①―②得文科數學.files/image407.gif) 即
即文科數學.files/image409.gif)
當文科數學.files/image411.gif) 時,
時,文科數學.files/image413.gif) ,當
,當文科數學.files/image415.gif) 時,
時,文科數學.files/image417.gif)
文科數學.files/image419.gif)
于是文科數學.files/image421.gif)
設存在正整數文科數學.files/image181.gif) ,使對
,使對文科數學.files/image424.gif) 恒成立
恒成立
當文科數學.files/image411.gif) 時,
時,文科數學.files/image427.gif) ,即
,即文科數學.files/image429.gif)
當文科數學.files/image415.gif) 時,
時,文科數學.files/image432.gif)
文科數學.files/image434.gif)
文科數學.files/image279.gif) 當
當文科數學.files/image437.gif) 時,
時,文科數學.files/image439.gif) 當
當文科數學.files/image441.gif) 時,
時,文科數學.files/image443.gif) ,當
,當文科數學.files/image445.gif) 時,
時,文科數學.files/image447.gif)
文科數學.files/image279.gif) 存在正整數
存在正整數文科數學.files/image450.gif) 或8,對于任意正整數
或8,對于任意正整數文科數學.files/image117.gif) 都有
都有文科數學.files/image453.gif) 成立。
成立。
www.ks5u.com
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com