
題目列表(包括答案和解析)
探究問題
(1)閱讀理解:
①如圖1,在△ABC所在平面上存在一點P,使它到三角形三頂點的距離之和最小,則稱點P為△ABC的費馬點,此時PA+PB+PC的值為△ABC的費馬距離.
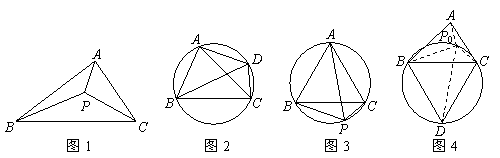 ②如圖2,若四邊形ABCD的四個頂點在同一個圓上,則有AB·CD+BC·AD=AC·BD.此為托勒密定理.
②如圖2,若四邊形ABCD的四個頂點在同一個圓上,則有AB·CD+BC·AD=AC·BD.此為托勒密定理.
(2)知識遷移:
①請你利用托勒密定理,解決如下問題:
如圖3,已知點P為等邊△ABC外接圓的弧BC上任意一點.求證:PB+PC=PA.
②根據(2)①的結論,我們有如下探尋△ABC(其中∠A、∠B、∠C均小于120º)的費馬點和費馬距離的方法:
第一步:如圖4,在△ABC的外部以BC為邊長作等邊△BCD及其外接圓;
第二步:在弧BC上取一點P0,連接P0A、P0B、P0C、P0D.
易知P0A+P0B+P0C=P0A+(P0B+P0C)=P0A+ ;
第三步:請你根據(1)①中定義,在圖4中找出△ABC的費馬點P,線段 的長度即為△ABC的費馬距離.
(3)知識應用:
2010年4月,我國西南地區出現了罕見的持續干旱現象,許多村莊出現了人、畜飲水困難.為解決老百姓飲水問題,解放軍某部到云南某地打井取水.
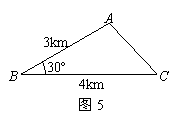 已知三村莊A、B、C構成了如圖5所示的△ABC(其中∠A、∠B、∠C均小于120º),現選取一點P打水井,使水井P到三村莊A、B、C所鋪設的輸水管總長度最小.求輸水管總長度的最小值.
已知三村莊A、B、C構成了如圖5所示的△ABC(其中∠A、∠B、∠C均小于120º),現選取一點P打水井,使水井P到三村莊A、B、C所鋪設的輸水管總長度最小.求輸水管總長度的最小值.



湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com