
題目列表(包括答案和解析)
(本題滿分18分)第(1)小題滿分5分,第(2)小題滿分7分,第(3)小題滿分6分。
各項均為正數的數列![]() 的前
的前![]() 項和為
項和為![]() ,滿足
,滿足![]() 。
。
 (1)求數列
(1)求數列![]() 的通項公式;
的通項公式;
(2)若數列![]() 滿足
滿足![]() ,數列
,數列![]() 滿足
滿足 ,數列
,數列![]() 的前
的前![]() 項和為
項和為![]() ,求
,求![]() ;
;
(3)若數列![]() ,甲同學利用第(2)問中的
,甲同學利用第(2)問中的![]() ,試圖確定
,試圖確定![]() 的值是否可以等于2011?為此,他設計了一個程序(如圖),但乙同學認為這個程序如果被執行會是一個“死循環”(即程序會永遠循環下去,而無法結束),你是否同意乙同學的觀點?請說明理由。
的值是否可以等于2011?為此,他設計了一個程序(如圖),但乙同學認為這個程序如果被執行會是一個“死循環”(即程序會永遠循環下去,而無法結束),你是否同意乙同學的觀點?請說明理由。
(本題滿分18分;第(1)小題5分,第(2)小題5分,第(3)小題8分)
設數列![]() 是等差數列,且公差為
是等差數列,且公差為![]() ,若數列
,若數列![]() 中任意(不同)兩項之和仍是該數列中的一項,則稱該數列是“封閉數列”.
中任意(不同)兩項之和仍是該數列中的一項,則稱該數列是“封閉數列”.
(1)若![]() ,求證:該數列是“封閉數列”;
,求證:該數列是“封閉數列”;
(2)試判斷數列![]() 是否是“封閉數列”,為什么?
是否是“封閉數列”,為什么?
(3)設![]() 是數列
是數列![]() 的前
的前![]() 項和,若公差
項和,若公差![]() ,試問:是否存在這樣的“封閉數列”,使
,試問:是否存在這樣的“封閉數列”,使 ;若存在,求
;若存在,求![]() 的通項公式,若不存在,說明理由.
的通項公式,若不存在,說明理由.
(本題滿分18分;第(1)小題5分,第(2)小題5分,第(3)小題8分)
設數列 是等差數列,且公差為
是等差數列,且公差為 ,若數列
,若數列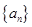 中任意(不同)兩項之和仍是該數列中的一項,則稱該數列是“封閉數列”.
中任意(不同)兩項之和仍是該數列中的一項,則稱該數列是“封閉數列”.
(1)若 ,求證:該數列是“封閉數列”;
,求證:該數列是“封閉數列”;
(2)試判斷數列 是否是“封閉數列”,為什么?
是否是“封閉數列”,為什么?
(3)設 是數列
是數列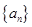 的前
的前 項和,若公差
項和,若公差 ,試問:是否存在這樣的“封閉數列”,使
,試問:是否存在這樣的“封閉數列”,使 ;若存在,求
;若存在,求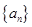 的通項公式,若不存在,說明理由.
的通項公式,若不存在,說明理由.
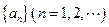 是等差數列,且公差為
是等差數列,且公差為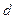 ,若數列
,若數列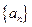 中任意(不同)兩項之和仍是該數列中的一項,則稱該數列是“封閉數列”.
中任意(不同)兩項之和仍是該數列中的一項,則稱該數列是“封閉數列”.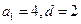 ,求證:該數列是“封閉數列”;
,求證:該數列是“封閉數列”;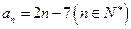 是否是“封閉數列”,為什么?
是否是“封閉數列”,為什么?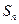 是數列
是數列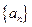 的前
的前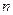 項和,若公差
項和,若公差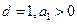 ,試問:是否存在這樣的“封閉數列”,使
,試問:是否存在這樣的“封閉數列”,使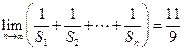 ;若存在,求
;若存在,求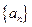 的通項公式,若不存在,說明理由.
的通項公式,若不存在,說明理由.(本題16分,第(1)小題3分;第(2)小題5分;第(3)小題8分)
已知數列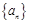 和
和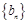 的通項分別為
的通項分別為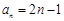 ,
,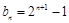 (
(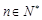 ),集合
),集合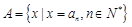 ,[來源:Zxxk.Com]
,[來源:Zxxk.Com]
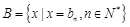 ,設
,設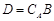 . 將集合
. 將集合 中元素從小到大依次排列,構成數列
中元素從小到大依次排列,構成數列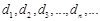 .
.
(1)寫出 ;
;
(2)求數列 的前
的前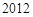 項的和;
項的和;
(3)是否存在這樣的無窮等差數列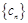 :使得
:使得 (
(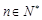 )?若存在,請寫出一個這樣的
)?若存在,請寫出一個這樣的
數列,并加以證明;若不存在,請說明理由.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com