日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

函數(shù)是奇函數(shù)，則q等于

A．kp (kÎZ)        B．kp+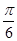(kÎZ)       C．kp+(kÎZ)      D．kp－(kÎZ)

已知二次函數(shù)f(x)=x²+ax（）．

（1）若函數(shù)y=f(sinx+cosx)(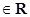)的最大值為，求f(x)的最小值；

（2）當(dāng)a>2時(shí),求證：f(sin²xlog₂sin²x+cos²xlog₂cos²x)1–a.其中x∈R,x¹kp且x¹kp(k∈Z).

已知函數(shù)f(x)＝cos(2x＋)＋－＋sinx·cosx

⑴ 求函數(shù)f(x)的單調(diào)減區(qū)間；       ⑵ 若xÎ[0,]，求f(x)的最值；

 ⑶ 若f(a)＝，2a是第一象限角，求sin2a的值.

【解析】第一問(wèn)中，利用f(x)＝cos2x－sin2x－cos2x＋sin2x＝sin2x－cos2x＝sin(2x－)令＋2kp≤2x－≤＋2kp，

解得＋kp≤x≤＋kp 

第二問(wèn)中，∵xÎ[0, ]，∴2x－Î[－,]，

∴當(dāng)2x－＝－，即x＝0時(shí)，f(x)_min＝－,

當(dāng)2x－＝， 即x＝時(shí)，f(x)_max＝1

第三問(wèn)中，(a)＝sin(2a－)＝,2a是第一象限角,即2kp＜2a＜＋2kp

∴ 2kp－＜2a－＜＋2kp,∴ cos(2a－)＝

利用構(gòu)造角得到sin2a＝sin[(2a－)＋]

解：⑴ f(x)＝cos2x－sin2x－cos2x＋sin2x     ………2分

＝sin2x－cos2x＝sin(2x－)                 ……………………3分

⑴ 令＋2kp≤2x－≤＋2kp，

解得＋kp≤x≤＋kp          ……………………5分

∴ f(x)的減區(qū)間是[＋kp,＋kp](kÎZ)            ……………………6分

⑵ ∵xÎ[0, ]，∴2x－Î[－,]，           ……………………7分

∴當(dāng)2x－＝－，即x＝0時(shí)，f(x)_min＝－,        ……………………8分

當(dāng)2x－＝， 即x＝時(shí)，f(x)_max＝1          ……………………9分

⑶ f(a)＝sin(2a－)＝,2a是第一象限角,即2kp＜2a＜＋2kp

∴ 2kp－＜2a－＜＋2kp,∴ cos(2a－)＝,   ……………………11分

∴ sin2a＝sin[(2a－)＋]

＝sin(2a－)·cos＋cos(2a－)·sin   ………12分

＝×＋×＝

（08年赤峰二中模擬理） 在下列關(guān)于函數(shù)y =sin2x + cos2x的結(jié)論中, 正確的是

A. 在區(qū)間[-+ kp, + kp](k Î Z)上是增函數(shù)       B. 周期是

C. 最大值為1, 最小值為- 1                          D. 是奇函數(shù)