日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

解：：因?yàn)?img width=364 height=41 src="http://thumb.zyjl.cn/pic1/1899/sx/151/231751.gif">，所以f(1)f(2)<0，因此f(x)在區(qū)間（1，2）上存在零點(diǎn)，又因?yàn)閥=與y=-在（0，+）上都是增函數(shù)，因此在（0，+）上是增函數(shù)，所以零點(diǎn)個(gè)數(shù)只有一個(gè)方法2：把函數(shù)的零點(diǎn)個(gè)數(shù)個(gè)數(shù)問題轉(zhuǎn)化為判斷方程解的個(gè)數(shù)問題，近而轉(zhuǎn)化成判斷與交點(diǎn)個(gè)數(shù)問題，在坐標(biāo)系中畫出圖形

由圖看出顯然一個(gè)交點(diǎn)，因此函數(shù)的零點(diǎn)個(gè)數(shù)只有一個(gè)

袋中有50個(gè)大小相同的號(hào)牌，其中標(biāo)著0號(hào)的有5個(gè)，標(biāo)著n號(hào)的有n個(gè)（n=1,2,…9）,現(xiàn)從袋中任取一球，求所取號(hào)碼的分布列，以及取得號(hào)碼為偶數(shù)的概率.

15．解：根據(jù)條件去畫滿足條件的二次函數(shù)圖象就可判斷出

某大型超市為促銷商品，特舉辦“購(gòu)物搖獎(jiǎng)100％中獎(jiǎng)”活動(dòng)，凡消費(fèi)者在該超市購(gòu)物滿20元，享受一次搖獎(jiǎng)機(jī)會(huì)，購(gòu)物滿40元，享受兩次搖獎(jiǎng)機(jī)會(huì)，依次類推。搖獎(jiǎng)機(jī)的旋轉(zhuǎn)圓盤是均勻的，扇形區(qū)域A、B、C、D、E所對(duì)應(yīng)的圓心角的比值分別為1:2:3:4:5。相應(yīng)區(qū)域分別設(shè)立一、二、三、四、五等獎(jiǎng)，獎(jiǎng)金分別為5元、4元、3元、2元、1元。求某人購(gòu)物３０元，獲得獎(jiǎng)金的分布列.

(1)列舉法：把集合中的元素　　　　　出來，寫在　　　　　內(nèi)表示集合的方法.列舉法表示集合的特點(diǎn)是清晰、直觀.集合中元素的個(gè)數(shù)較少時(shí)常適用于列舉法.?

(2)描述法：把集合中的元素　　　　　的描述出來，寫在　　　　　內(nèi)表示集合的方法.一般形式是{x|p}，其中豎線前面的x叫做此集合的代表元素，豎線后面的p指出元素x所具有的公共屬性.描述法便于從整體上把握一個(gè)集合，常適用于集合中元素的公共屬性較為明顯時(shí).

(3)韋恩圖：為了形象地表示集合，有時(shí)常用一些封閉的　　　　　表示一個(gè)集合，這樣的圖形稱為韋恩圖，在解題時(shí)，利用韋恩圖“數(shù)”和“形”結(jié)合，使得解答十分直觀.?

如集合A={a，b，c}可形象地表示為圖(1)或圖(2).?

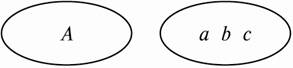
                        (1)　　　　            　　(2)

解關(guān)于的不等式

【解析】本試題主要考查了含有參數(shù)的二次不等式的求解，

首先對(duì)于二次項(xiàng)系數(shù)a的情況分為三種情況來討論，

A=0,a>0,a<0,然后結(jié)合二次函數(shù)的根的情況和圖像與x軸的位置關(guān)系，得到不等式的解集。

解：①若a=0，則原不等式變?yōu)?2x+2<0即x>1

此時(shí)原不等式解集為；   

②若a>0，則ⅰ）時(shí)，原不等式的解集為；

ⅱ）時(shí)，原不等式的解集為；

  ⅲ）時(shí)，原不等式的解集為。 

③若a<0，則原不等式變?yōu)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012070911034560884068/SYS201207091104230776185555_ST.files/image013.png">

    原不等式的解集為。

 

解析　第二列等式的右端分別是1×1,3×3,6×6,10×10,15×15，∵1,3,6,10,15，…第n項(xiàng)a_n與第n－1項(xiàng)a_n－1(n≥2)的差為：a_n－a_n－1＝n，∴a₂－a₁＝2，a₃－a₂＝3，a₄－a₃＝4，…，a_n－a_n－1＝n，各式相加得，

a_n＝a₁＋2＋3＋…＋n，其中a₁＝1，∴a_n＝1＋2＋3＋…＋n，即a_n＝，∴a＝n²(n＋1)².

答案　n²(n＋1)²