日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

查看答案和解析>>

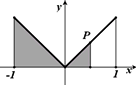
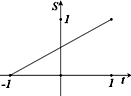
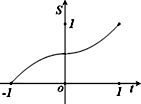
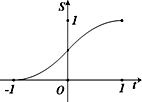
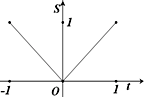
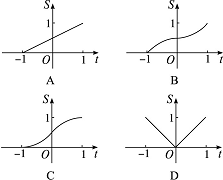
在函數y＝|x|(x∈[－1,1])的圖象上有一點P(t，|t|)，此函數與x軸、直線x＝－1及x＝t圍成圖形(如圖陰影部分)的面積為S，則S與t的函數關系圖象可表示為(　　)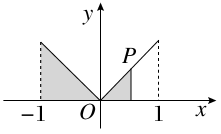

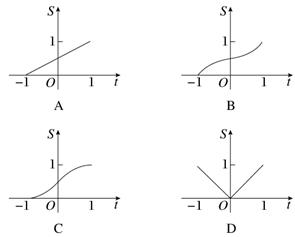
查看答案和解析>>

查看答案和解析>>

在函數y＝|x|(x∈[－1，1])的圖象上有一點P(t|t|)，此函數與x軸、直線x＝－1及x＝t圍成圖形(如圖陰影部分)的面積為S，則S與t的函數關系圖可表示為

[　　]

A．

B．

C．

D．

查看答案和解析>>

查看答案和解析>>

1.A　2.B　3.A　4.C　5.C　6.B　7.D　8.B　9.B　10.D　11.B　12.D

13.－3　14.7　15.②④　16.3

17.解：(1)f(x)＝Acos²(ωx＋φ)＋1＝cos(2ωx＋2φ)＋＋1.

又A＞0，ω＞0,0＜φ＜，∴f(x)的最大值為A＋1，最小值為1.

由f(x)的最大值與最小值的差為2，∴A＝2.

由f(x)過點(0,2)，f(0)＝cos 2φ＋2＝2，∴φ＝，

則T＝4π＝，∴ω＝，f(x)＝cos(x＋)＋2＝2－sinx.6分

(2)∵B＝，∴b＝f(B)＝2－sin(?)＝.

設A，C所對的邊分別為a，c，由余弦定理得＝a²＋c²－2accos，＋ac＝a²＋c²≥2ac，ac≤，

當且僅當a＝c＝時等號成立，△ABC的面積S＝acsin≤.12分

18.解：(1)某應聘者能被聘用的概率為p₀＝1－(1－)(1－)(1－p)＝＋p.4分

(2)在4位應聘者中恰好有2人被聘用的概率為CP?(1－P₀)²，

恰有3位被聘用的概率為Cp?(1－p₀)¹，依題意Cp?(1－p₀)²≥Cp?(1－p₀)¹，解得p₀≤，

即＋p≤⇒0≤p≤.12分

19.解：(1)連AQ，∠PQA是PQ與平面ABCD所成角，AQ＝2，BQ＝2，即Q是BC的中點，過Q作QH⊥AD于H，則QH⊥平面PAD，過Q作QM⊥PD，連MH，則∠QMH為所求二面角的平面角.

在Rt△PAD中，＝⇒MH＝＝＝，

所以tan∠QMH＝＝＝，

從而所求二面角的大小為arctan .6分

(2)由于Q是BC的中點，可得DQ⊥PQ，

⇒面PAQ⊥面PDQ，

過A作AG⊥PQ于G，則AG為點A到平面PQD的距離.

AG＝＝＝.12分

另解：分別以AD，AB，AP為x，y，z軸建立空間直角坐標系，

由條件知Q是BC的中點，面PAD的一個法向量是＝(0,2,0).

又D(4,0,0)，Q(2,2,0)，P(0,0,4)，

故＝(0,2,0)，＝(－4,0,4)，

設面PDQ的法向量為n＝(x，y，z)，

則⇒由此可取n＝(1,1,1)，

從而(1)cos〈，n〉＝＝＝.

(2)面PDQ的一個法向量為n＝(1,1,1)，＝(2,2,0)，

故點A到平面PDQ的距離d＝＝＝.

20.解：(1)a_n＋1＝a_n－1＋(－1)^n－1＋n，于是a₃＝a₁＋2－1＝2，a_2n－1＝a_2n－3－1＋2n－2(n≥2)，

∴a_2n－1＝a_2n－3＋2n－3(n≥2).

…………

a₃＝a₁＋1

a_2n－1＝a₁＋＝n²－2n＋2.2分

而a₂＝b₁＋1＝2

a₄＝b₃＋3＝a₂＋4

…………

a_2n＝a_2n－2＋2n

∴a_2n＝a_2n－2＋2n

∴a_2n＝a₂＋＝n²＋n.8分

(2)S_n＝＋＋…＋

＝＋＋…＋＝1－

∴S₂₀₀₉＝1－＝.12分

21.解：(1)設P(x，y)，則＝(－2－x，－y)，＝(2－x，－y)，依題意有(－2－x)(2－x)＋y²＝?，化簡得x²－y²＝2.4分

(2)假設存在定點F(m,0)，使?為常數.

當直線l與x軸不垂直時，設l：y＝k(x－2)，

⇒(1－k²)x²＋4k²x－4k²－2＝0，

依題意k²≠1，設M(x₁，y₁)，N(x₂，y₂)，則

于是?＝(x₁－m，y₁)(x₂－m，y₂)＝(k²＋1)x₁x₂－(2k²＋m)(x₁＋x₂)＋4k²＋m²

＝＋m²－4m＋2.8分

要使?是與k無關的常數，當且僅當m＝1，此時?＝－1.

當直線l⊥x軸時，可得M(2，)，N(2，－)，若m＝1，則?＝(1，)(1，－)＝－1.

所以在x軸上存在定點F(1,0)，使?為常數.12分

22.解：f′(x)＝4x³＋3ax²＋4x＝x(4x²＋3ax＋4).

(1)當a＝－時，f′(x)＝4x³＋3ax²＋4x＝2x(2x－1)(x－2)，令f′(x)≥0，得0≤x≤或x≥2，所以f(x)的增區間為[0，]與[2，＋∞).4分

(2)f′(x)＝x(4x²＋3ax＋4)，顯然x＝0不是方程4x²＋3ax＋4＝0的根，為使f(x)僅在x＝0處有極值，4x²＋3ax＋4≥0必須恒成立，即有Δ＝9a³－64≤0，解得a∈[－，].8分

(3)由條件a∈[－2,2]知Δ＝9a²－64＜0，從而4x²＋3ax＋4＞0恒成立.

當x＜0時f′(x)＜0；當x＞0時，f′(x)＞0.

因此f(x)在區間[－1,1]上的最大值為max{f(－1)，f(1)}.

為使對任意a∈[－2,2]，f(x)≤1在x∈[－1,1]上恒成立，當且僅當⇒在a∈[－2,2]上恒成立，解得b≤－4，故b的取值范圍是(－∞，－4].