
題目列表(包括答案和解析)
已知 是數列{
是數列{ }的前n項和,并且
}的前n項和,并且 =1,對任意正整數n,
=1,對任意正整數n, ;設
;設 ).(I)證明數列
).(I)證明數列 是等比數列,并求
是等比數列,并求 的通項公式;
的通項公式;
(II)設 的前n項和,求
的前n項和,求 .
.
已知數列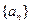 的首項
的首項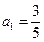 ,
,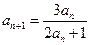 ,
,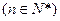 .
.
(1)求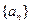 的通項公式;
的通項公式;
(2)證明:對任意的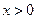 ,
,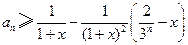 ,
,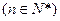 ;
;
(3)證明: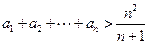 .
.
設數列 前
前 項和為
項和為 ,且
,且 。其中
。其中 為實常數,
為實常數, 且
且 。
。
(1)求證: 是等比數列;
是等比數列;
(2)若數列 的公比滿足
的公比滿足 且
且 ,求
,求 的
的
通項公式;
(3)若 時,設
時,設 ,是否存在最大的正整數
,是否存在最大的正整數 ,使得對任意
,使得對任意 均有
均有 成立,若存在求出
成立,若存在求出 的值,若不存在請說明理由。
的值,若不存在請說明理由。
(08年洛陽市統一考試文)(12分) 數列![]() 是公差
是公差![]() 的等差數列,且
的等差數列,且![]() 。
。
(1)求![]() 的通項公式;
的通項公式;
(2)求數列![]() 的前n項和Sn。
的前n項和Sn。
一、
|