
題目列表(包括答案和解析)
(本小題滿分13分)設函數![]() ,其中
,其中![]() .(1)若
.(1)若![]() ,求
,求![]() 的單調遞增區間;(2)如果函數
的單調遞增區間;(2)如果函數![]() 在定義域內既有極大值又有極小值,求實數
在定義域內既有極大值又有極小值,求實數![]() 的取值范圍;(3)求證對任意的
的取值范圍;(3)求證對任意的![]() ,不等式
,不等式![]() 恒成立
恒成立
(08年安徽卷理)(本小題滿分13分)
設數列![]() 滿足
滿足![]() ,其中
,其中![]() 為實數。
為實數。
(Ⅰ)證明:![]() 對任意
對任意![]() 成立的充分必要條件是
成立的充分必要條件是![]() ,
,
(Ⅱ)設![]() ,證明:
,證明:![]() ;
;
(Ⅲ)設![]() ,證明:
,證明:![]()
(本小題滿分13分)
設函數 ,其中
,其中 ,且a≠0.
,且a≠0.
(Ⅰ)當a=2時,求函數 在區間[1,e]上的最小值;
在區間[1,e]上的最小值;
(Ⅱ)求函數 的單調區間。
的單調區間。
(本小題滿分13分)設函數 ,其中
,其中![]() 表示不超過
表示不超過![]() 的最大整數,如
的最大整數,如![]() . (Ⅰ)求
. (Ⅰ)求![]() 的值; (Ⅱ)若在區間
的值; (Ⅱ)若在區間![]() 上存在x,使得
上存在x,使得![]() 成立,求實數k的取值范圍;(Ⅲ)求函數
成立,求實數k的取值范圍;(Ⅲ)求函數![]() 的值域.
的值域.
(本小題滿分13分) 設數列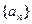 是公比大于1的等比數列,
是公比大于1的等比數列, 為其前
為其前 項和,已知
項和,已知 =7且
=7且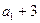 ,
, ,
,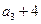 成等差數列.
成等差數列.
(1)求數列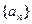 的通項公式;
的通項公式;
(2)設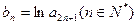 ,求數列
,求數列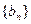 的前
的前 項和
項和 
(3)求 的表達式.
的表達式.
1、B 2、B 3、D 4、D 5、A 6、D 7、B 8、C 9、A 10、B
11、.files/image216.gif) 12、
12、.files/image218.gif) 13、
13、.files/image220.gif) 14
14.files/image222.gif) 、15、
、15、.files/image224.gif) 16、
16、.files/image226.gif) -
-.files/image228.gif) ,0
,0.files/image230.gif)
17. 解:(1)∵.files/image232.gif) ,
,
∴.files/image234.gif) ,
,
∵.files/image236.gif) ,∴
,∴.files/image238.gif) ,∴
,∴.files/image240.gif) ,
,
∴.files/image242.gif) 。………………………………….6分
。………………………………….6分
(2)∵.files/image244.gif) ,
,
.files/image246.gif) ,
,
∴.files/image248.gif) ,
,
∵.files/image236.gif) ,∴
,∴.files/image238.gif) ,∴
,∴.files/image250.gif) ,∴
,∴.files/image252.gif) …….12分
…….12分
18、.files/image175.gif) 的所有可能取值有6,2,1,-2;
的所有可能取值有6,2,1,-2;.files/image255.gif) ,
,.files/image257.gif)
.files/image259.gif) ,
,.files/image261.gif)
故.files/image175.gif) 的分布列為:
的分布列為:
.files/image175.gif)
6
2
1
-2
.files/image264.gif)
0.63
0.25
0.1
0.02
(2).files/image266.gif)
(3)設技術革新后的三等品率為.files/image155.gif) ,則此時1件產品的平均利潤為
,則此時1件產品的平均利潤為
.files/image269.gif)
依題意,.files/image271.gif) ,即
,即.files/image273.gif) ,解得
,解得.files/image275.gif) 所以三等品率最多為
所以三等品率最多為.files/image277.gif)
19、(Ⅰ)證明:因為.files/image279.gif) 所以
所以.files/image281.gif) ′(x)=x2+2x,
′(x)=x2+2x,
x
(-∞,-2)
-2
(-2,0)
0
(0,+∞)
f′(x)
+
0
-
0
+
f(x)
ㄊ
極大值
ㄋ
極小值
ㄊ
由點.files/image283.gif) 在函數y=f′(x)的圖象上,
在函數y=f′(x)的圖象上,
又.files/image285.gif) 所以
所以.files/image287.gif)
所以.files/image289.gif) ,又因為
,又因為.files/image281.gif) ′(n)=n2+2n,所以
′(n)=n2+2n,所以.files/image292.gif) ,
,
故點.files/image294.gif) 也在函數y=f′(x)的圖象上.
也在函數y=f′(x)的圖象上.
(Ⅱ)解:.files/image296.gif) ,
,
由.files/image298.gif) 得
得.files/image300.gif) .
.
當x變化時,.files/image302.gif) ?
?.files/image042.gif) 的變化情況如下表:
的變化情況如下表:
注意到.files/image305.gif) ,從而
,從而
①當.files/image307.gif) ,此時
,此時.files/image042.gif) 無極小值;
無極小值;
②當.files/image310.gif) 的極小值為
的極小值為.files/image312.gif) ,此時
,此時.files/image042.gif) 無極大值;
無極大值;
③當.files/image315.gif) 既無極大值又無極小值.
既無極大值又無極小值.
20、(Ⅰ)證明:由四邊形ABCD為菱形,∠ABC=60°,可得△ABC為正三角形.
因為 E為BC的中點,所以AE⊥BC.
又 BC∥AD,因此AE⊥AD.
因為PA⊥平面ABCD,AE.files/image317.gif) 平面ABCD,所以PA⊥AE.
平面ABCD,所以PA⊥AE.
而 PA.files/image317.gif) 平面PAD,AD
平面PAD,AD.files/image317.gif) 平面PAD 且PA∩AD=A,
平面PAD 且PA∩AD=A,
所以 AE⊥平面PAD,又PD.files/image317.gif) 平面PAD.
平面PAD.
.files/image319.gif) 所以 AE⊥PD.
所以 AE⊥PD.
(Ⅱ)解:設AB=2,H為PD上任意一點,連接AH,EH.
由(Ⅰ)知 AE⊥平面PAD,
則∠EHA為EH與平面PAD所成的角.
在Rt△EAH中,AE=.files/image321.gif) ,
,
所以 當AH最短時,∠EHA最大,
即 當AH⊥PD時,∠EHA最大.
此時 tan∠EHA=.files/image323.gif)
因此 AH=.files/image325.gif) .又AD=2,所以∠ADH=45°,
.又AD=2,所以∠ADH=45°,
所以 PA=2.
解法一:因為 PA⊥平面ABCD,PA.files/image317.gif) 平面PAC,
平面PAC,
所以 平面PAC⊥平面ABCD.
過E作EO⊥AC于O,則EO⊥平面PAC,
過O作OS⊥AF于S,連接ES,則∠ESO為二面角E-AF-C的平面角,
在Rt△AOE中,EO=AE?sin30°=.files/image327.gif) ,AO=AE?cos30°=
,AO=AE?cos30°=.files/image329.gif) ,
,
又F是PC的中點,在Rt△ASO中,SO=AO?sin45°=.files/image331.gif) ,
,
又 .files/image333.gif)
.files/image335.gif)
在Rt△ESO中,cos∠ESO=.files/image337.gif)
即所求二面角的余弦值為.files/image339.gif)
21、(Ⅰ)解:依題設得橢圓的方程為.files/image341.gif) ,
,
直線.files/image343.gif) 的方程分別為
的方程分別為.files/image345.gif) ,
,.files/image347.gif) .??????????????????????????????????? 2分
.??????????????????????????????????? 2分
如圖,設.files/image349.gif) ,其中
,其中.files/image351.gif) ,
,
.files/image352.gif) 且
且.files/image354.gif) 滿足方程
滿足方程.files/image356.gif) ,
,
故.files/image358.gif) .①
.①
由.files/image195.gif) 知
知.files/image361.gif) ,得
,得.files/image363.gif) ;
;
由.files/image365.gif) 在
在.files/image367.gif) 上知
上知.files/image369.gif) ,得
,得.files/image371.gif) .
.
所以.files/image373.gif) ,
,
化簡得.files/image375.gif) ,
,
解得.files/image377.gif) 或
或.files/image379.gif) .??????????????????????????????????????????????????????????????????????????????? 6分
.??????????????????????????????????????????????????????????????????????????????? 6分
(Ⅱ)解法一:根據點到直線的距離公式和①式知,點.files/image381.gif) 到
到.files/image367.gif) 的距離分別為
的距離分別為.files/image384.gif) ,
,
.files/image386.gif) .??????????????????????????????????????????????????? 9分
.??????????????????????????????????????????????????? 9分
又.files/image388.gif) ,所以四邊形
,所以四邊形.files/image198.gif) 的面積為
的面積為
.files/image391.gif)
.files/image393.gif)
.files/image395.gif)
.files/image397.gif)
.files/image399.gif) ,
,
當.files/image401.gif) ,即當
,即當.files/image403.gif) 時,上式取等號.所以
時,上式取等號.所以.files/image405.gif) 的最大值為
的最大值為.files/image407.gif) .?????????????????????? 12分
.?????????????????????? 12分
解法二:由題設,.files/image409.gif) ,
,.files/image411.gif) .
.
設.files/image413.gif) ,
,.files/image415.gif) ,由①得
,由①得.files/image417.gif) ,
,.files/image419.gif) ,
,
故四邊形.files/image198.gif) 的面積為
的面積為
.files/image422.gif)
.files/image424.gif) ????????????????????????????????????????????????????????????????????????????????????????????? 9分
????????????????????????????????????????????????????????????????????????????????????????????? 9分
.files/image426.gif)
.files/image428.gif)
.files/image430.gif)
.files/image432.gif) ,
,
當.files/image434.gif) 時,上式取等號.所以
時,上式取等號.所以.files/image405.gif) 的最大值為
的最大值為.files/image407.gif) . 12分
. 12分
22、解法一:(Ⅰ).files/image438.gif) ,
,.files/image440.gif) ,
,.files/image442.gif) ,
,
又.files/image444.gif) ,
,.files/image446.gif) 是以
是以.files/image448.gif) 為首項,
為首項,.files/image450.gif) 為公比的等比數列.
為公比的等比數列.
.files/image452.gif)
.files/image454.gif) ,
,.files/image456.gif) .
.
(Ⅱ)由(Ⅰ)知.files/image458.gif) ,
,
.files/image460.gif)
.files/image462.gif)
.files/image464.gif)
.files/image466.gif)
.files/image468.gif)
.files/image470.gif) ,
,.files/image452.gif) 原不等式成立.
原不等式成立.
(Ⅲ)由(Ⅱ)知,對任意的.files/image209.gif) ,有
,有
.files/image474.gif)
.files/image476.gif)
.files/image478.gif) .
.
.files/image452.gif) 取
取.files/image481.gif) ,
,
則.files/image483.gif) .
.
.files/image452.gif) 原不等式成立.
原不等式成立.
解法二:(Ⅰ)同解法一.
(Ⅱ)設.files/image486.gif) ,
,
則.files/image488.gif)
.files/image490.gif) ,
,
.files/image452.gif) 當
當.files/image493.gif) 時,
時,.files/image495.gif) ;當
;當.files/image497.gif) 時,
時,.files/image499.gif) ,
,
.files/image452.gif) 當
當.files/image502.gif) 時,
時,.files/image042.gif) 取得最大值
取得最大值.files/image505.gif) .
.
.files/image452.gif) 原不等式成立.
原不等式成立.
(Ⅲ)同解法一.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com