題目列表(包括答案和解析)
（05天津卷）19．土星周圍有美麗壯觀的“光環”，組成環的顆粒是大小不等、線度從1μm到10m的巖石、塵埃，類似于衛星，它們與土星中心的距離從7.3×104km延伸到1.4×105km。已知環的外緣顆粒繞土星做圓周運動的周期約為14h，引力常量為6.67×10-11NŸm2/kg2，則土星的質量約為（估算時不考慮環中顆粒間的相互作用）
Ａ．9.0×1016kg Ｂ．6.4×1017kg Ｃ．9.0×1025kg Ｄ．6.4×1026kg
（05年天津卷）土星周圍有美麗壯觀的“光環”，組成環的顆粒是大小不等、線度從1μm到10m的巖石、塵埃，類似于衛星，它們與土星中心的距離從7.3×104km延伸到1.4×105km。已知環的外緣顆粒繞土星做圓周運動的周期約為14h，引力常量為6.67×10-11NŸm2/kg2，則土星的質量約為（估算時不考慮環中顆粒間的相互作用）
Ａ．9.0×1016kg Ｂ．6.4×1017kg Ｃ．9.0×1025kg Ｄ．6.4×1026kg
分享到百度分享
一個有一定厚度的圓盤，可以繞通過中心垂直于盤面的水平軸轉動，用下面的方法測量它勻速轉動時的角速度。
實驗器材：電磁打點計時器、米尺、紙帶、復寫紙片。
實驗步驟：
（1）如圖1所示，將電磁打點計時器固定在桌面上，將紙帶的一端穿過打點計時器的限位孔后，固定在待測圓盤的側面上，使得圓盤轉動時，紙帶可以卷在圓盤側面上。
（2）啟動控制裝置使圓盤轉動，同時接通電源，打點計時器開始打點。
（3）經過一段時間，停止轉動和打點，取下紙帶，進行測量。
① 由已知量和測得量表示的角速度的表達式為ω= 。式中各量的意義是：
.
② 某次實驗測得圓盤半徑r=5.50×10-2m，得到紙帶的一段如圖2所示，求得角速度為 。
（1） （2）6.8/s。 |
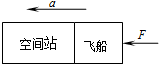如圖所示是采用動力學方法測量空間站質量的原理圖，若已知飛船質量為3.0×103kg，其推進器的平均推力為900N，在飛船與空間站對接后，推進器工作5s內，測出飛船和空間站速度變化是0.05m/s，則空間站的質量為（ ）| A．9.0×104kg | B．8.7×104kg | C．6.0×104kg | D．6.0×103kg |
14． A 15． A 16．C 17．A D 18．B D 19．A D 20．D 21．B
22． Ⅰ．單分子 ，36～40
Ⅱ.①29.9kΩ，(3分)②(a )外接，分壓 (3分) (b )見下圖，(3分)③變小(3分)
 |
|||
 |
|||
23．解：水從h高處落下可認為是自由落體運動，速度為v，則
（2分）
m/s ①
（2分）
設在很短時間t內有質量為m的水落到石頭上，以它為研究對象，設石頭對水的平均作用力為F，取豎直向下為正方向，由動量定理得，
②，而
③ （6分）
由①②③式代入數據解得，
N（2分）
根據牛頓第三定律可知，水對石頭的反作用力
=N．
（2分）
24． 解：（1）小球由靜止到最低點時，有
（2分）
（1分）
小球與物塊Q相撞時: 
，（1分） 
，（1分）
解得，
，
（2分）
Q在平板車上滑行的過程中，有
（1分）
（1分）
小物塊Q離開平板車時，速度為
（1分）
（2）由能的轉化和守恒定律，知
（1分）
（1分） 解得，
（1分）
（3）小物塊Q在平板車上滑行過程中，對地位移為s，則:
（1分） 解得，
（1分）
平拋時間
（1分） 水平距離
（1分）
Q落地點距小球的水平距離為
（1分）
25．解:（1）在0―t0帶電粒子做勻速圓周運動其周期為
（2分）
則在t0時間內轉過的圓心角 
位置坐標：
（4分）
（2）t0―2t0時間內帶電粒子做勻速直線運動，2t0―3t0時間內帶電粒子做勻速圓周運動，
轉過的圓心角仍為
；……．所以粒子從出發到再次回到原點所用的時間為t=8t0．（3分）
由于帶電粒子的速率不會改變，所以帶電粒子從出發到再次回到原點的運動軌跡的
長度s=8 v0t0．（3分）
（3）由帶電粒子的比荷
可知粒子運動的周期 
（2分）
則在t0時間內轉過的圓心角 
t0時刻粒子第一次到達x軸速度方向沿y軸負方向，則在t0―2t0時間內沿y軸負方向做勻加速直線運動；在2t0―3t0時間內帶電粒子又做勻速圓周運動，轉過的圓心角仍為
，由于速度增大，因此，此時運動的軌道半徑大于第一次時的半徑．在3t0―4t0時間內，帶電粒子沿y軸正方向做勻減速直線運動，第二次到達x軸由對稱性可知，在4t0時速度又變為v0；在4t0―5t0時間內又做圓周運動，第三次到達x軸時在坐標原點，設帶電粒子在x軸上方做圓周運動的軌道半徑為r1，在x軸下方做圓周運動的軌道半徑為r2，由幾何關系可知，要使帶電粒子回到原點，則必須滿足：
（2分） 
解得：
（2分）
又由于 
（2分） 解得：
（2分）
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
，T為電磁打點計時器打點的時間間隔，r為圓盤的半徑，x2、x1是紙帶上選定的兩點分別對應的米尺的刻度值，n為選定的兩點間的打點數（含兩點）。
或
……；（s5+s6）/2T；1，5
