
題目列表(包括答案和解析)
我市某高中的一個綜合實踐研究小組欲研究晝夜溫差大小與患感冒人數多少之間的關系,他們分別到氣象局與某醫院抄錄了1至6月份每月10號的晝夜溫差情況與因患感冒而就診的人數,得到如下資料:
| 日 期 | 1月10日 | 2月10日 | 3月10日 | 4月10日 | 5月10日 | 6月10日 |
晝夜溫差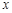 (°C) (°C) | 10 | 11 | 13 | 12 | 8 | 6 |
就診人數 (個) (個) | 22 | 25 | 29 | 26 | 16 | 12 |
 關于
關于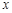 的線性回歸方程
的線性回歸方程 .
.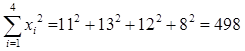 ;
;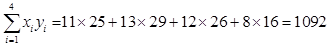 .
.| 日 期 | 1月10日 | 2月10日 | 3月10日 | 4月10日 | 5月10日 | 6月10日 |
晝夜溫差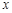 (°C) (°C) | 10 | 11 | 13 | 12 | 8 | 6 |
就診人數 (個) (個) | 22 | 25 | 29 | 26 | 16 | 12 |
 關于
關于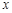 的線性回歸方程
的線性回歸方程 .
. ;
; .
.已知![]() ,且方程f(x)+4x-8=0有兩個不同的正根,其中一根是另一根的3倍,記等差數列{an}、{bn}的前項和分別為Sn,Tn且
,且方程f(x)+4x-8=0有兩個不同的正根,其中一根是另一根的3倍,記等差數列{an}、{bn}的前項和分別為Sn,Tn且![]() (n∈N+).
(n∈N+).

(1)若![]() ,求g(n)的最大值;
,求g(n)的最大值;
(2)若![]() ,數列{bn}的公差為3,試問在數列{an}與{bn}中是否存在相等的項,若存在,求出由這些相等項從小到大排列得到的數列{cn}的通項公式;若不存在,請說明理由.
,數列{bn}的公差為3,試問在數列{an}與{bn}中是否存在相等的項,若存在,求出由這些相等項從小到大排列得到的數列{cn}的通項公式;若不存在,請說明理由.
(3)若![]() ,數列{bn}的公差為3,且
,數列{bn}的公差為3,且![]() ,
,![]() .試證明:
.試證明:![]() .
.
已知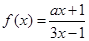 ,且方程
,且方程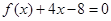 有兩個不同的正根,其中一根是另一根的
有兩個不同的正根,其中一根是另一根的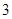 倍,記等差數列
倍,記等差數列 、
、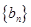 的前
的前 項和分別為
項和分別為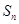 ,
, 且
且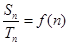 (
(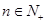 )。
)。
(1)若 ,求
,求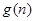 的最大值;
的最大值;
(2)若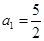 ,數列
,數列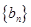 的公差為3,試問在數列
的公差為3,試問在數列 與
與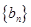 中是否存在相等的項,若存在,求出由這些相等項從小到大排列得到的數列
中是否存在相等的項,若存在,求出由這些相等項從小到大排列得到的數列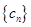 的通項公式;若不存在,請說明理由.
的通項公式;若不存在,請說明理由.
(3)若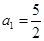 ,數列
,數列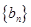 的公差為3,且
的公差為3,且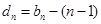 ,
,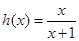 .
.
試證明: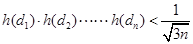 .
.
下表是我國一個工業城市每年中度以上污染的天數,由于以前只注重經濟發展,沒有過多的考慮工業發展對環境的影響,近幾年來,該市加大了對污染企業的治理整頓,環境不斷得到改善。
|
年份(x) |
2005年 |
2006年 |
2007年 |
2008年 |
2009年 |
|
中度以上污染的天數(y) |
90 |
74 |
62 |
54 |
45 |
(1)請根據上表提供的數據,用最小二乘法求出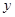 關于
關于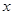 的線性回歸方程
的線性回歸方程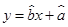 ;
;
(2)按照環境改善的趨勢,估計2012年中度以上污染的天數。
(3)在以上5年中任取2年,至少有1年中度以上污染的天數小于60天的概率有多大。
(可用公式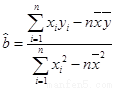 ,
, 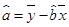 )
)
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com