日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

已知△的內角所對的邊分別為且.

 (1) 若, 求的值;

(2) 若△的面積 求的值.

【解析】本小題主要考查正弦定理、余弦定理、同角三角函數的基本關系等基礎知識，考查運算求解能力。第一問中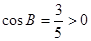，得到正弦值，再結合正弦定理可知，，得到（2）中即所以c=5,再利用余弦定理，得到b的值。

解: (1)∵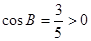, 且,   ∴ .        由正弦定理得，    ∴.    

   (2)∵       ∴.   ∴c=5      

由余弦定理得，

∴

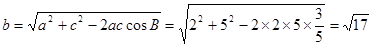
在△ABC中，角A、B、C的對邊分別為a、b、c，向量=（sinA,b+c），=（a－c,sinC－sinB）,滿足=

（Ⅰ）求角B的大小；

（Ⅱ）設=（sin（C+）,）, =（2k,cos2A） （k>1）,  有最大值為3，求k的值.

【解析】本試題主要考查了向量的數量積和三角函數，以及解三角形的綜合運用

第一問中由條件|p +q |=| p －q |，兩邊平方得p·q＝0，又

p=（sinA,b+c）,q=（a－c,sinC－sinB）,代入得（a－c）sinA＋（b+c）（sinC－sinB）＝0，

根據正弦定理，可化為a（a－c）+（b+c）（c－b）=0,

即，又由余弦定理＝2acosB,所以cosB＝，B＝

第二問中，m=（sin（C+）,）,n=（2k,cos2A） （k>1）,m·n=2ksin（C+）+cos2A=2ksin（C+B） +cos2A

=2ksinA+-=-+2ksinA+=-+ （k>1）.

而0<A<,sinA∈（0,1],故當sin＝1時，m·n取最大值為2k-=3,得k＝.