題目列表(包括答案和解析)
| |||||
| |||||
| 1 |
| x |
| f(x2)-f(x1) |
| x2-x1 |
| 1 |
| x |
| f(x2)-f(x1) |
| x2-x1 |
定義：已知函數f（x）與g（x），若存在一條直線y=kx +b，使得對公共定義域內的任意實數均滿足g（x）≤f（x）≤kx+b恒成立，其中等號在公共點處成立，則稱直線y=kx +b為曲線f（x）與g（x）的“左同旁切線”．已知
（I）證明：直線y=x-l是f（x）與g（x）的“左同旁切線”；
（Ⅱ）設P（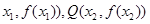
是函數 f（x）圖象上任意兩點，且0<x1<x2，若存在實數x3>0，使得
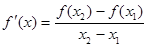．請結合（I）中的結論證明：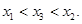
1．C 2．C 3．B 4．A 5．C 6．C 7．D 8．C 9．D 10．B 
1l．B 12．A
2．解析：
，∴選C．
3．解析：
是增函數 
故
，即
又
，故選B．
4．解析：如圖作出可行域，作直線
，平移直線
至
位置，使其經過點
．此時目標函數取得最大值（注意
與
反號）
由
得
，故選A
5．解析：設有人投中為事件，則
，
故選C．
6．解析：
展開式中通項；
由
，得
，故選C．
7．解析：
由
得
，故選D．
8．略
9．解析：由
得準線方程
，雙曲線準線方程為
，解得
，
，故選D．
10．解析：設正四面體的棱長為2，取
中點為
，連接
，則
為
與
所成的角，在
中
，故選B．
11．解析：
由題意
，則
，故選B．
12．解析：由已知
，
為球的直么
，又
，
設
，則
，
又由
，解得
，故選A．
另法：將四面體
置于正方休中．
正方體的對角線長為球的直徑，由此得
，然后可得
．
二、填空題
13．3；解析：
在
上的投影是
．
14．（0．2）；解析：由
，解得
．
15．
解析：
，
由余弦定理
為鈍角
，即
，
解得．
16．②③；
解析：容易知命題①是錯的，命題②、③都是對的，對于命題④我們考查如圖所示的正方體，政棱長為
，顯然
與
為平面
內兩條距離為的平行直線，它們在底面內的射影
、
仍為兩條距離為的平行直線．但兩平面與卻是相交的．
三、
17．解：（1）
，
，
即
，故
．
（2）
由
得
．
設邊上的高為
。則
．
18．（1）設甲、乙兩人同時參加災區服務為事件，則
．
（2）記甲、乙兩人同時參加同一災區服務為事件
，那么
．
19．解：
（1）
平面
∵二面角
為直二面角，且
，
平面
平面
．
（2）（法一）連接
交交于
點，連接
是邊長為2的正方形， 
，
平面
，由三垂線定理逆定理得
是二面角
的平面角
由（1）
平面
，
．
在
中，
∴在
中，
故二面角等于
．
（2）（法二）利用向量法，如圖以之中點
為坐標原點建立空間坐標系
，則
，
設平面的法向量分別為
，則由
得
，而平面
的一個法向理
故所求二面角等于
．
20．解：（1）由題設
，即
易知
是首項為
，公差為2的等差數列，
∴通項公式為
，
（2）由題設，
，得
是以
公比為
的等比數列．
由
得
．
21．解：（1）由題意
，由拋物線定義可求得曲線
的方程為
．
（2）證明：設點、的坐標分別為
若直線有斜率時，其坐標滿足下列方程組：
， 
若沒有斜率時，方程為
．
又
．
；又
，
．
22．（1）解：方程
可化為
．
當
時，
，又
，于是
，解得
，故
．
（2）解：設
為曲線上任一點，由
知曲線在點處的切線方程為
，即
．
令
，得
，從而得切線與直線的交點坐標為
令
，得
，從而得切線與直線
的交點坐標為
．所以點處的切線與直線
所圍成的三角形面積為
．故曲線
上任一點處的切線與直線所圍成的三角形的面積為定值，此定值為6．
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
．請結合(I)中的結論證明：x1＜x3＜x2．
．請結合(Ⅰ)中的結論證明：x1＜x3＜x2．