
題目列表(包括答案和解析)
以原點O及點A(5,2)為頂點作等腰直角三角形OAB,使![]() ,則
,則![]() 的坐標為( )。
的坐標為( )。
A、(2,-5) B、(-2,5)或(2,-5)
C、(-2,5) D、(7,-3)或(3,7)
以O為原點,![]() 所在直線為
所在直線為![]() 軸,建立如 所示的坐標系。設
軸,建立如 所示的坐標系。設![]() ,點F的坐標為
,點F的坐標為![]() ,
,![]() ,點G的坐標為
,點G的坐標為![]() 。
。
(1)求![]() 關于
關于![]() 的函數
的函數![]() 的表達式,判斷函數
的表達式,判斷函數![]() 的單調性,并證明你的判斷;
的單調性,并證明你的判斷;
(2)設ΔOFG的面積![]() ,若以O為中心,F為焦點的橢圓經過點G,求當
,若以O為中心,F為焦點的橢圓經過點G,求當![]() 取最小值時橢圓的方程;
取最小值時橢圓的方程;
(3)在(2)的條件下,若點P的坐標為![]() ,C、D是橢圓上的兩點,且
,C、D是橢圓上的兩點,且![]() ,求實數
,求實數![]() 的取值范圍。
的取值范圍。
從原點出發的某質點M,按向量a=(0,1)移動的概率為![]() ,按向量b=(0,2)移動的概率為
,按向量b=(0,2)移動的概率為![]() ,設M可到達點(0,n)的概率為Pn
,設M可到達點(0,n)的概率為Pn
(1)求P1和P2的值;(2)求證:![]() =
=![]() ;(3)求
;(3)求![]() 的表達式。
的表達式。
為了得到函數 的圖象,只要把函數
的圖象,只要把函數 的圖象上所有點的
的圖象上所有點的
A. 橫坐標縮短到原來的 倍(縱坐標不變),再把所得圖象上所有的點向左平移
倍(縱坐標不變),再把所得圖象上所有的點向左平移 個單位長度。
個單位長度。
B. 橫坐標伸長到原來的2倍(縱坐標不變),再把所得圖象上所有點的向左平移 個單位長度。
個單位長度。
C. 向右平移 個單位長度,再把所得圖象上所有的點橫坐標縮短到原來的
個單位長度,再把所得圖象上所有的點橫坐標縮短到原來的 倍(縱坐標不變)
倍(縱坐標不變)
D. 向左平移 個單位長度,再把所得圖象上所有點的橫坐標伸長到原來的2倍(縱坐標不變)
個單位長度,再把所得圖象上所有點的橫坐標伸長到原來的2倍(縱坐標不變)
(本小題滿分12分)已知函數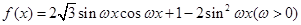 ,
,
且函數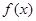 的最小正周期為
的最小正周期為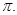
(1)若 ,求函數
,求函數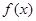 的單調遞減區間;
的單調遞減區間;
(2)將函數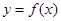 的圖象上各點的縱坐標保持不變,橫坐標縮短到原來的
的圖象上各點的縱坐標保持不變,橫坐標縮短到原來的 ,把所得到的圖象再向左平移
,把所得到的圖象再向左平移 個單位,得到函數
個單位,得到函數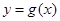 的圖象,求函數
的圖象,求函數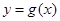 在區間
在區間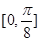 上的最小值。
上的最小值。
一、選擇題(4′×10=40分)
題號
1
2
3
4
5
6
7
8
9
10
答案
D
D
B
C
D
C
A
A
B
A
三、填空題(4′×4=16分)
11.
 12.
12. 13.
13. 14.
14.
三、解答題(共44分)
15.①解:原不等式可化為: ………………………2′
………………………2′
 作根軸圖:
作根軸圖:
………………………4′
可得原不等式的解集為: ………………………6′
………………………6′
②解:直線 的斜率
的斜率 ………………………2′
………………………2′
∵直線 與該直線垂直
與該直線垂直
∴ 則
則 的方程為:
的方程為: ………………………4′
………………………4′
即 為所求………………………6′
為所求………………………6′
16.解:∵ 則
則 ,
, 且
且 ………………………1′
………………………1′
∴有 ………………………3′
………………………3′
 ………………………4′
………………………4′
 ………………………5′
………………………5′

當且僅當: 即
即 ………………………5′
………………………5′
亦: 時取等號
時取等號
所以:當 時,
時, ………………………7′
………………………7′
17.解:將 代入
代入 中變形整理得:
中變形整理得:
 ………………………2′
………………………2′
首先
 且
且 ………………………3′
………………………3′
設

由題意得:
解得: 或
或 (舍去)………………………6′
(舍去)………………………6′
由弦長公式得: ………………………8′
………………………8′
18.解①設雙曲線的實半軸,虛半軸分別為 ,
,

則有: ∴
∴ ………………………1′
………………………1′
于是可設雙曲線方程為: ①或
①或 ②………………………3′
②………………………3′
將點 代入①求得:
代入①求得:
將點 代入②求得:
代入②求得: (舍去) ………………………4′
(舍去) ………………………4′
∴ ,
, 
∴雙曲線的方程為: ………………………5′
………………………5′
②由①解得: ,
, ,
, ,焦點在
,焦點在 軸上………………………6′
軸上………………………6′
∴雙曲線的準線方程為: ………………………7′
………………………7′
漸近線方程為:  ………………………8′
………………………8′
19.解:①設 為橢圓的半焦距,則
為橢圓的半焦距,則 ,
,
∵ ∴
∴ ∴
∴ ………………………1′
………………………1′
將 代入
代入 ,可求得
,可求得
 ∵
∵ ∴
∴
即 又
又 、
、 ………………………3′
………………………3′
∴ ,
,
∵ ………………………5′
………………………5′
∴
從而
∴離心率 ………………………6′
………………………6′
②由拋物線的通徑
得拋物線方程為 ,其焦點為
,其焦點為 ………………………7′
………………………7′
∴橢圓的左焦點
∴
由①解得:
∴ ………………………8′
………………………8′
∴該橢圓方程為: ………………………9′
………………………9′
③
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com