
題目列表(包括答案和解析)
 的兩個焦點為F1(-c,0),F2(c,0),M是橢圓上的一點,且滿足
的兩個焦點為F1(-c,0),F2(c,0),M是橢圓上的一點,且滿足 .
. ;
;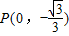 、Q的直線對稱?若能,求出k的取值范圍;若不能,請說明理由.
、Q的直線對稱?若能,求出k的取值范圍;若不能,請說明理由. 的兩個焦點為F1(-c,0),F2(c,0),M是橢圓上的一點,且滿足
的兩個焦點為F1(-c,0),F2(c,0),M是橢圓上的一點,且滿足 .
. ;
; 、Q的直線對稱?若能,求出k的取值范圍;若不能,請說明理由.
、Q的直線對稱?若能,求出k的取值范圍;若不能,請說明理由. 的兩個焦點為F1(-c,0),F2(c,0),M是橢圓上的一點,且滿足
的兩個焦點為F1(-c,0),F2(c,0),M是橢圓上的一點,且滿足 .
. ;
; 、Q的直線對稱?若能,求出k的取值范圍;若不能,請說明理由.
、Q的直線對稱?若能,求出k的取值范圍;若不能,請說明理由. 的兩個焦點為F1(-c,0),F2(c,0),M是橢圓上的一點,且滿足
的兩個焦點為F1(-c,0),F2(c,0),M是橢圓上的一點,且滿足 .
. ;
; 、Q的直線對稱?若能,求出k的取值范圍;若不能,請說明理由.
、Q的直線對稱?若能,求出k的取值范圍;若不能,請說明理由.設橢圓 的中心和拋物線
的中心和拋物線 的頂點均為原點
的頂點均為原點 ,
, 、
、 的焦點均在
的焦點均在 軸上,過
軸上,過 的焦點F作直線
的焦點F作直線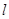 ,與
,與 交于A、B兩點,在
交于A、B兩點,在 、
、 上各取兩個點,將其坐標記錄于下表中:
上各取兩個點,將其坐標記錄于下表中: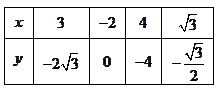

(1)求 ,
, 的標準方程;
的標準方程;
(2)若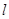 與
與 交于C、D兩點,
交于C、D兩點,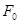 為
為 的左焦點,求
的左焦點,求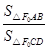 的最小值;
的最小值;
(3)點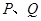 是
是 上的兩點,且
上的兩點,且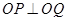 ,求證:
,求證: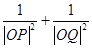 為定值;反之,當
為定值;反之,當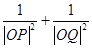 為此定值時,
為此定值時,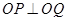 是否成立?請說明理由.
是否成立?請說明理由.
1.B 2.C 3.B 4.C 5.B 6.B 7.C 8.B 9.C 10.B 
11.C 12.D
【解析】
3.當 時,函數
時,函數 在
在 上,
上, 恒成立即
恒成立即 在
在 上恒成立,可得
上恒成立,可得

當 時,函數
時,函數 在
在 上,
上, 恒成立
恒成立
即 在
在 上恒成立
上恒成立
可得 ,對于任意
,對于任意 恒成立
恒成立
所以 ,綜上得
,綜上得 .
.
4.解法一:聯立 ,得
,得 .
.
 方程總有解,需
方程總有解,需 恒成立
恒成立
即 恒成立,得
恒成立,得 恒成立
恒成立
 ;又
;又

 的取值范圍為
的取值范圍為 .
.
解法二:數形結合,因為直線 恒過定點(0,1),要使直線與橢圓
恒過定點(0,1),要使直線與橢圓 總有交點當日僅當點(0,1)在橢圓上或橢圓內,即
總有交點當日僅當點(0,1)在橢圓上或橢圓內,即

 又
又

 的取值范圍為
的取值范圍為 .
.
5.

7.展開式前三項的系數滿足 可解得
可解得 ,或
,或 (舍去).從而可知有理項為
(舍去).從而可知有理項為 ,故C正確.
,故C正確.
8. ,欲使
,欲使 為奇函數,須使
為奇函數,須使 ,觀察可知,
,觀察可知, 、
、 不符合要求,若
不符合要求,若 ,則
,則
 ,其在
,其在 上是減函數,故B正確
上是減函數,故B正確
當 時,
時, ,其在
,其在 上是增函數,不符合要求.
上是增函數,不符合要求.
9. 等價于
等價于

畫圖可知 ,故
,故 .
.
10.如圖乙所示.設 ,點
,點 到直線
到直線 的距離為
的距離為 ,則由拋物線定義得
,則由拋物線定義得 ,
,

又由點 在橢圓上,及橢圓第一定義得
在橢圓上,及橢圓第一定義得
由橢圓第二定義得 ,解之得
,解之得 .
.
11.從52張牌中任意取13張牌的全部取法為 ;缺少某一種花色的取法為
;缺少某一種花色的取法為 ,缺少兩種花色的取法為
,缺少兩種花色的取法為 ,缺少三種花色的取法為
,缺少三種花色的取法為 ,根據容斥原理可知四種花色齊全的取法為
,根據容斥原理可知四種花色齊全的取法為 .
.
12.設 中點為
中點為 ,連
,連 .由已知得
.由已知得 平面
平面 ,作
,作 ,交
,交 的延長線于點
的延長線于點 ,連
,連 .則
.則 為所求,設
為所求,設 ,則
,則 ,在
,在
中可求出 ,則
,則 .
.
二、填空題
13. .
.
提示:可以用換元法,原不等式為 也可以用數形結合法.
也可以用數形結合法.
令 ,在同一坐標系內分別畫出這兩個函數的圖象,由圖直觀得解集.
,在同一坐標系內分別畫出這兩個函數的圖象,由圖直觀得解集.
14.12 .提示:經判斷,
.提示:經判斷, 為截面團的直徑,再由巳知可求出球的半徑為
為截面團的直徑,再由巳知可求出球的半徑為 .
.
15. .提示:由于
.提示:由于 得
得
解得 ,又
,又

所以,當 時,
時, 取得最小值.
取得最小值.
16.①②④
三、解答題
17.懈:
 ,由正弦定理得,
,由正弦定理得,

 又
又 ,
,
 ,化簡得
,化簡得
 為等邊三角形.
為等邊三角形.
說明;本題是向量和三角相結合的題目,既考查了向量的基本知識,又考查了三角的有關知識,三角形的形狀既可由角確定。也可由邊確定,因此既可從角入手,把邊化為角;也可從邊入手,把角化為邊來判斷三角形的形狀.
18.解:(1)在第一次更換燈泡工作中,不需要更換燈泡的概率為 需要更換2只燈泡的概率為
需要更換2只燈泡的概率為 .
.
(2)對該盞燈來說,在第1、2次都更換了燈泡的概率為 ,在第一次未更換燈泡而在第二次需要更換燈泡的概率為
,在第一次未更換燈泡而在第二次需要更換燈泡的概率為 ,故所求的概率為
,故所求的概率為 .
.
(3)當 時,
時,
由(2)知第二次燈泡更換工作中,某盞燈更換的概率
故至少換4只燈泡的概率為



19.解: ]
]
因為函數 在
在 處的切線斜率為
處的切線斜率為
所以
即 ①
①
又
得 ②
②
(1)函數 在
在 時有極值
時有極值
 ③
③
解式①②③得
所以 .
.
(2)因為函數 在區間
在區間 上單調遞增,所以導函數
上單調遞增,所以導函數 在區間
在區間 的值恒大于或等于零.
的值恒大于或等于零.
則
得 ,所以實數
,所以實數 的取值范圍為
的取值范圍為 .
.
20.解:(1)連接 因為
因為 平面
平面 ,平面
,平面 平面
平面
所以 ;又
;又 為
為 的中點,故
的中點,故 為
為 的中點
的中點

 底面
底面
 為
為 與底面
與底面 所成的角
所成的角
在 中,
中,

 所以
所以 與底面
與底面 所成的角為45°.
所成的角為45°.
(2)解法一;如圖建立直角坐標系
則 ,
, 
 設
設 點的坐標為
點的坐標為
故



 點
點 的坐標為
的坐標為

故 .
.
解法二: 平面
平面
 ,又
,又
 平面
平面
在正方形 中,
中,
 .
.
21.解:(1)設點 、
、 的坐標分別為
的坐標分別為 、
、 ,點
,點 的坐標為
的坐標為
當 時,設直線
時,設直線 的斜率為
的斜率為
 直線
直線 過點
過點
 的方程為
的方程為
又已知 ①
①
 ②
②
 ③
③
 ④
④
∴式①一式②得
 ⑤
⑤
③式+式④得
 ⑥
⑥
∴由式⑤、式⑥及
得點 的坐標滿足方程
的坐標滿足方程
 ⑦
⑦
當 時,
時, 不存在,此時
不存在,此時 平行于
平行于 軸,因此
軸,因此 的中點
的中點 一定落在
一定落在 軸上,即
軸上,即 的坐標為
的坐標為 ,顯然點
,顯然點 (
( ,0)滿足方程⑦
,0)滿足方程⑦
綜上,點 的坐標滿足方程
的坐標滿足方程
設方程⑦所表示的曲線為
則由 ,
,
得
因為 ,又已知
,又已知 ,
,
所以當 時.
時. ,曲線
,曲線 與橢圓
與橢圓 有且只有一個交點
有且只有一個交點 ,
,
當 時,
時, ,曲線
,曲線 與橢圓
與橢圓 沒有交點,因為(0,0)在橢圓內,又在曲線
沒有交點,因為(0,0)在橢圓內,又在曲線 上,所以曲線
上,所以曲線 在橢圓內,故點
在橢圓內,故點 的軌跡方程為
的軌跡方程為

(2)由 解得曲線
解得曲線 與
與 軸交于點(0,0),(0,
軸交于點(0,0),(0, )
)
由 解得曲線
解得曲線 與
與 軸交于點(0,0).(
軸交于點(0,0).( ,0)
,0)
當 ,即點
,即點 為原點時,(
為原點時,( ,0)、(0,
,0)、(0, )與(0.0)重合,曲線
)與(0.0)重合,曲線 與坐標軸只有一個交點(0,0).
與坐標軸只有一個交點(0,0).
當 ,且
,且 ,即點
,即點 不在橢圓
不在橢圓 外且在除去原點的
外且在除去原點的 軸上時,曲線
軸上時,曲線 與坐標軸有兩個交點(0,
與坐標軸有兩個交點(0, )與(0,0),同理,當
)與(0,0),同理,當 且
且 時,曲線與坐標軸有兩個交點(
時,曲線與坐標軸有兩個交點( ,o)、(0,0).
,o)、(0,0).
當 ,且
,且 時,即點
時,即點 不在橢圓
不在橢圓 且不在坐標軸上時,曲線與坐標軸有三個交點(
且不在坐標軸上時,曲線與坐標軸有三個交點( ,0)、(0,
,0)、(0, )與(0,0).
)與(0,0).
22.(1)解: ,又
,又
 是以首項為
是以首項為 ,公比為
,公比為 的等比數列.
的等比數列.
 .
.
(2)證明:設數列 的公比為
的公比為 ,則條件等式可化為:
,則條件等式可化為:
 數列
數列 為等差數列,
為等差數列,
(3)證明:由題意知
 ①
①
式① 得
得
 ②
②
式①-式②得



 .
.
www.ks5u.com
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com