
題目列表(包括答案和解析)



 的通項公式;
的通項公式; ,若
,若 對
對 恒成立,求實數
恒成立,求實數 的取值范圍;
的取值范圍; 為首項,公比為
為首項,公比為 的數列
的數列 ,
, ,使得數列
,使得數列 中每一項都是數列
中每一項都是數列 中不同的項,若存在,求出所有滿足條件的數列
中不同的項,若存在,求出所有滿足條件的數列 的通項公式;若不存在,說明理由
的通項公式;若不存在,說明理由數列![]() 的通項公式
的通項公式![]()
![]()
(1)求:f(1)、f(2)、f(3)、f(4)的值;
(2)由上述結果推測出計算f(n)的公式,并用數學歸納法加以證明.
設數列![]() 的通項公式為
的通項公式為![]() 。數列
。數列![]() 定義如下:對于正整數m,
定義如下:對于正整數m,![]() 是使得不等式
是使得不等式![]() 成立的所有n中的最小值。 (1)若
成立的所有n中的最小值。 (1)若![]() ,求b3; (2)若
,求b3; (2)若![]() ,求數列
,求數列![]() 的前2m項和公式;(3)是否存在p和q,使得
的前2m項和公式;(3)是否存在p和q,使得![]() ?如果存在,求p和q的取值范圍;如果不存在,請說明理由。
?如果存在,求p和q的取值范圍;如果不存在,請說明理由。
設數列![]() 的通項公式為
的通項公式為![]() 。數列
。數列![]() 定義如下:對于正整數m,
定義如下:對于正整數m,![]() 是使得不等式
是使得不等式![]() 成立的所有n中的最小值。
成立的所有n中的最小值。
(1)若![]() ,求b3;
,求b3;
(2)若![]() ,求數列
,求數列![]() 的前2m項和公式;
的前2m項和公式;
(3)是否存在p和q,使得![]() ?如果存在,求p和q的取值范圍;如果不存在,請說明理由。
?如果存在,求p和q的取值范圍;如果不存在,請說明理由。
設數列 的通項公式為
的通項公式為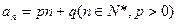 。數列
。數列 定義如下:對于正整數m,
定義如下:對于正整數m, 是使得不等式
是使得不等式 成立的所有n中的最小值。 (1)若
成立的所有n中的最小值。 (1)若 ,求b3; (2)若
,求b3; (2)若 ,求數列
,求數列 的前2m項和公式;(3)是否存在p和q,使得
的前2m項和公式;(3)是否存在p和q,使得 ?如果存在,求p和q的取值范圍;如果不存在,請說明理由。
?如果存在,求p和q的取值范圍;如果不存在,請說明理由。
一、選擇題:BCDC DCAB
二、填空題:
9.153 10. 11.
11. 12.
12.
13. 14.
14. 15. 8
15. 8
三.解答題
16.(1) ,
, ,
,
(2)

17.(1)
(2)
 ,當
,當 或13時,
或13時,
18.(1)略 (2)
(3)若存在P,使 ,矛盾。
,矛盾。
19.

當 ,即
,即 時,
時,
20.(1)
(2)


(3) 或
或 ,又
,又
21.(1)

(2)
先猜想(取特殊法位置):
再證: ,對符合條件的B都成立。
,對符合條件的B都成立。
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com