
題目列表(包括答案和解析)
(本題滿分12分)
如下圖,某地有三家工廠,分別位于矩形ABCD 的頂點A、B 及CD的中點P 處,已知AB=20km,CB =10km ,為了處理三家工廠的污水,現要在矩形ABCD 的區域上(含邊界),且與A、B等距離的一點O處建造一個污水處理廠,并鋪設排污管道AO、BO、OP ,設排污管道的總長度為 km.
km.
(1)按下列要求寫出函數關系式:
①設∠BAO=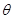 (rad),將
(rad),將 表示成
表示成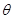 的函數;
的函數;
②設OP (km) ,將
(km) ,將 表示成
表示成 的函數.
的函數.
(2)請選用(1)中的一個函數關系式,確定污水處理廠的位置,使鋪設的排污管道總長度最短.
(本題滿分12分) (I)對于計算![]() 值的一個算法,其算法步驟如下:
值的一個算法,其算法步驟如下:
第一步,令![]()
第二步,若 (1) 成立,則執行第三步;否則,輸出![]() ,并結束算法 。
,并結束算法 。
第三步,計算![]()
第四步,計算![]() ,返回第二步。
,返回第二步。
在算法步驟中 (1) 處填上合適的條件,使之能完成該題算法功能(請寫在答題卷上);
(II)畫出輸入一個正整數![]() ,求
,求![]() 值的程序框圖。
值的程序框圖。
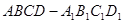 中,
中,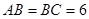 ,用過
,用過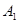 ,
,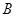 ,
,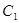 三點的平面截去長方體的一個角后,留下如圖的幾何體,且這幾何體的體積為120.
三點的平面截去長方體的一個角后,留下如圖的幾何體,且這幾何體的體積為120.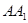 的長;
的長;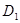 到平面
到平面 的距離.
的距離.
(本題滿分12分)
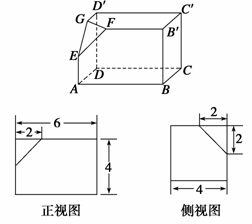
如下的三個圖中,上面的是一個長方體截去一個角所得多面體的直觀圖,它的正視圖和側視圖在下面畫出(單位: )
)
(Ⅰ)在正視圖下面,按照畫三視圖的要求畫出該多面體的俯視圖;
(Ⅱ)按照給出的尺寸,求該多面體的體積;
(Ⅲ)在所給直觀圖中連結 ,證明:
,證明: ∥面
∥面

(本題滿分12分)
如下的三個圖中,上面的是一個長方體截去一個角所得多面體的直觀圖,它的正視圖和側視圖在下面畫出(單位:![]() )
)
(Ⅰ)在正視圖下面,按照畫三視圖的要求畫出該多面體的俯視圖;
(Ⅱ)按照給出的尺寸,求該多面體的體積;
(Ⅲ)在所給直觀圖中連結![]() ,證明:
,證明:![]() ∥面
∥面![]()
一、選擇題
1.D. 2.A. 3.B. 4.C. 5.B. 6.A.
7.C. 8.D. 9.D. 10.C. 11.B. 12.B.
二、填空題:
13.%20數學文科.files/image161.gif) .
14.5. 15.
.
14.5. 15.%20數學文科.files/image163.gif) 或
或%20數學文科.files/image165.gif) . 16.②.
. 16.②.
三、解答題:本大題共6小題,共74分.解答應寫出文字說明.證明過程或演算步驟.
17.本題主要考查兩角和與差的三角函數公式、二倍角公式,三角函數的圖象與性質等基礎知識;考查運算求解能力.滿分12分.
%20數學文科.files/image167.gif)
%20數學文科.files/image169.gif)
%20數學文科.files/image171.gif) .
.
%20數學文科.files/image173.gif) ,
,
%20數學文科.files/image175.gif) ,
,
即%20數學文科.files/image177.gif) 時,f(x)單調遞增.
時,f(x)單調遞增.
∴f(x)的單調遞增區間為[%20數學文科.files/image179.gif) ,
,%20數學文科.files/image181.gif) ]
]%20數學文科.files/image183.gif) .
.
18.(1)記“編號的和為%20數學文科.files/image185.gif) ”的事件
”的事件%20數學文科.files/image187.gif) ,事件
,事件%20數學文科.files/image187.gif) 所包含的基本事件為
所包含的基本事件為%20數學文科.files/image190.gif) 、
、%20數學文科.files/image192.gif) 、
、%20數學文科.files/image194.gif) 、
、%20數學文科.files/image196.gif) 、
、%20數學文科.files/image198.gif) ,共5個, ∴
,共5個, ∴%20數學文科.files/image200.gif)
(2)記“甲贏”為事件%20數學文科.files/image202.gif) ,事件
,事件%20數學文科.files/image202.gif) 所包含的基本事件為
所包含的基本事件為%20數學文科.files/image205.gif) 、
、%20數學文科.files/image207.gif) 、
、%20數學文科.files/image190.gif) 、
、%20數學文科.files/image210.gif) 、
、%20數學文科.files/image192.gif) 、
、%20數學文科.files/image213.gif) 、
、%20數學文科.files/image194.gif) 、
、%20數學文科.files/image216.gif) 、
、%20數學文科.files/image196.gif) 、
、%20數學文科.files/image219.gif) 、
、%20數學文科.files/image198.gif) 、
、%20數學文科.files/image222.gif) 、
、%20數學文科.files/image224.gif) ,共13個, ∴
,共13個, ∴%20數學文科.files/image226.gif) ,
,
19.本題主要考查空間幾何體的直觀圖、三視圖,空間線面的位置關系等基礎知識;考查空間想像能力及推理論證能力.滿分12分.
(Ⅰ)如圖
%20數學文科.files/image228.jpg)
俯視圖
(Ⅱ)所求多面體的體積
%20數學文科.files/image230.gif) .
.
(Ⅲ)證明:如圖,在長方體%20數學文科.files/image232.gif) 中,連接
中,連接%20數學文科.files/image234.gif) ,則
,則%20數學文科.files/image234.gif) ∥
∥%20數學文科.files/image237.gif) .
.
%20數學文科.files/image239.jpg)
因為E,G分別為%20數學文科.files/image241.gif) 的中點,
的中點,
所以%20數學文科.files/image234.gif) ∥
∥%20數學文科.files/image243.gif) ,從而
,從而%20數學文科.files/image243.gif) ∥
∥%20數學文科.files/image237.gif) .
.
又%20數學文科.files/image246.gif) ,所以
,所以%20數學文科.files/image237.gif) ∥平面EFG.
∥平面EFG.
20. 本題主要考查等差數列、數列求和等基礎知識;考查推理論證與運算求解能力;考查化歸與轉化思想.滿分12分.
(Ⅰ)設數列{an}的公差為d,則
%20數學文科.files/image249.gif)
解得%20數學文科.files/image251.gif) .
.
因此,an=-1+2(n-1)=2n-3.
(Ⅱ)由已知%20數學文科.files/image143.gif) (1)得,
(1)得,
當n≥2時,%20數學文科.files/image253.gif) (2).
(2).
由(1)-(2)得%20數學文科.files/image255.gif) ,
,
所以%20數學文科.files/image257.gif) ,又
,又%20數學文科.files/image259.gif) ,
,
故%20數學文科.files/image261.gif) .
.
在式(1)中,令n=1得,%20數學文科.files/image263.gif) ,
,
又%20數學文科.files/image265.gif) ,故
,故%20數學文科.files/image267.gif) .
.
所以%20數學文科.files/image269.gif) .
.
21.本題主要考查直線與橢圓的位置關系等基礎知識;考查運算求解能力及化歸與轉化思想.滿分12分.
(Ⅰ)由題設b=%20數學文科.files/image149.gif) ,c=2,從而a2=b2+c2=6,
,c=2,從而a2=b2+c2=6,
所以橢圓C的方程為%20數學文科.files/image271.gif) .
.
(Ⅱ)假設斜率為k的直線l與橢圓C交于A、B兩點,使得∠AOB為銳角,
設直線l的方程為y=k(x - 2).
%20數學文科.files/image273.jpg)
%20數學文科.files/image275.jpg)
%20數學文科.files/image277.jpg)
所以滿足題意的的直線l存在,斜率k的取值范圍為%20數學文科.files/image279.gif)
方法二:
同方法一得到%20數學文科.files/image281.gif) .
.
%20數學文科.files/image283.jpg)
所以滿足題意的的直線l存在,斜率k的取值范圍為%20數學文科.files/image279.gif)
22.本題主要考查利用導數研究函數的性質,考查運算求解能力及數形結合思想.滿分14分.
(Ⅰ)%20數學文科.files/image285.gif) ,由
,由%20數學文科.files/image287.gif) 得,
得,
%20數學文科.files/image289.gif) ,解得
,解得%20數學文科.files/image291.gif) .
.
(Ⅱ)由(Ⅰ)知,
%20數學文科.files/image293.gif) ,
,
%20數學文科.files/image295.gif) .
.
當%20數學文科.files/image297.gif) 時,
時,%20數學文科.files/image299.gif) ;
;
當%20數學文科.files/image301.gif) 時,
時,%20數學文科.files/image303.gif) ;
;
%20數學文科.files/image305.gif) 時,
時,%20數學文科.files/image299.gif) .
.
所以%20數學文科.files/image154.gif) 的單調增區間是
的單調增區間是%20數學文科.files/image308.gif) ;
;%20數學文科.files/image154.gif) 的單調減區間是
的單調減區間是%20數學文科.files/image310.gif) .
.
(Ⅲ)由(Ⅱ)知,%20數學文科.files/image154.gif) 在
在%20數學文科.files/image312.gif) 內單調遞增,在
內單調遞增,在%20數學文科.files/image310.gif) 內單調遞減,在
內單調遞減,在%20數學文科.files/image315.gif) 上單調遞增,且當
上單調遞增,且當%20數學文科.files/image317.gif) 或
或%20數學文科.files/image319.gif) 時,
時,%20數學文科.files/image321.gif) .
.
所以%20數學文科.files/image154.gif) 的極大值為
的極大值為%20數學文科.files/image323.gif) ,極小值為
,極小值為%20數學文科.files/image325.gif) .
.
又因為%20數學文科.files/image327.gif) ,
,
%20數學文科.files/image329.gif) .
.
當且僅當%20數學文科.files/image331.gif) ,直線
,直線%20數學文科.files/image156.gif) 與
與%20數學文科.files/image334.gif) 的圖象有三個交點.
的圖象有三個交點.
所以,%20數學文科.files/image082.gif) 的取值范圍為
的取值范圍為%20數學文科.files/image336.gif) .
.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com