20090505
= 故選C
故選C
6. 提示: 如圖,取G的極端位置 , 問題轉化為求AE與
, 問題轉化為求AE與 的位置關系,取AD的中點M,連接MF、
的位置關系,取AD的中點M,連接MF、 可證
可證
 可見AE與FG所成的角為
可見AE與FG所成的角為 A故選D
A故選D
7. 提示: 當x>0時, 的圖像相同,故可排除(A)、(C)、(D).故選B
的圖像相同,故可排除(A)、(C)、(D).故選B
8. 令
令 =5,得3n=5r+10 , 當r=1時,n=5.故選C
=5,得3n=5r+10 , 當r=1時,n=5.故選C
9.提示由 ,得
,得 ,所以
,所以 , 點P的軌跡是圓(除去與直線AB的交點).故選B
, 點P的軌跡是圓(除去與直線AB的交點).故選B
10.提示:令f(x)= x2?(a2+b2?6b)x+ a2+b2+2a?4b+1,則由題意有f(0)= a2+b2+2a?6b+1≤0且f(1)=2a+2b+2≥0,即(a+1)2+(b?2)2≤4且a+b+1≥0,在直角坐標平面aOb上作出其可行域如圖所示,而a2+b2+4a=(a+2)2+b2?4的幾何意義為|PA|2?4(其中P(a,b)為可行域內任意的一點,A(?2,0)). 由圖可知,當P點在直線l:a+b+1=0上且AP⊥l時取得最小值;當P點為AC(C為圓(a+1)2+(b?2)2≤4的圓心)的延長線與圓C的交點時達到最大值. 又A點的直線l的距離為,|AC|=,所以a2+b2+4a的最大值和最小值分別為?和(+2)2?4=5+4.故選B.
11.提示: 易知數列{an}是以3為周期的數列,a1=2, a2=
 , a3=
, a3=  , a4 =2,
, a4 =2,
故 a2009= 故選B
故選B
12.提示: ∵ 是定義在R上的奇函數,
是定義在R上的奇函數,
∴ ,又由已知
,又由已知 ,
,
∴ ,(A)成立;
,(A)成立;
∵ ,
,
∴(B)成立;當 時
時 ,又
,又 為奇函數,
為奇函數,
∴ ,
, ,且
,且 ,
,
∴(C)即 ,
,
∴(C)成立;對于(D),有 ,由于
,由于 時
時 的符號不確定,
的符號不確定,
∴ 未必成立。故選D
未必成立。故選D
二、填空題:(本大題共4小題,每小題5分,共20分)
13.5;提示: Tr+1= (x
(x )n-r(-
)n-r(- )r,由題意知:-
)r,由題意知:- +
+ =27
=27 n=9
n=9
∴展開式共有10項,二項式系數最大的項為第五項或第六項,故項的系數最大的項為第五項。
14.(0,1)∪(1,10) ;提示: 當a>1時,不等式化為10-ax>a,要使不等式有解,必須10-a>0
∴1<a<10
當0<a<1時,不等式化為0<10-ax<a 10-a<ax<10不等式恒有解
10-a<ax<10不等式恒有解
故滿足條件a的范圍是(0,1)∪(1,10)
15. ;提示: P=1-
;提示: P=1- =
=
16.  提示:當直角三角形的斜邊垂直與平面時,所求面積最大。
提示:當直角三角形的斜邊垂直與平面時,所求面積最大。
三、解答題:(本大題共6小題,共70分)
17.(本大題10分)(1)不是,假設 是
是 在
在 上的生成函數,則
上的生成函數,則
存在正實數 使得
使得 恒成立,令
恒成立,令 ,得
,得 ,與
,與
矛盾,
所以函數 一定不是
一定不是 在
在 上的生成函數…………5分
上的生成函數…………5分
(2)設 ,因為
,因為 
所以 ,當且僅當
,當且僅當 且
且 時等號成立,
時等號成立,
即 時
時
而 ,
,


 …………………………………………10分
…………………………………………10分
18.(Ⅰ)連接A1C.∵A1B1C1-ABC為直三棱柱,
∴CC1⊥底面ABC,∴CC1⊥BC.
∵AC⊥CB,∴BC⊥平面A1C1CA. ……………1分
∴ 為
為 與平面A1C1CA所成角,
與平面A1C1CA所成角,
 .
.
∴ 與平面A1C1CA所成角為
與平面A1C1CA所成角為 .…………4分
.…………4分
(Ⅱ)分別延長AC,A1D交于G. 過C作CM⊥A1G 于M,連結BM,
∵BC⊥平面ACC1A1,∴CM為BM在平面A1C1CA內的射影,
∴BM⊥A1G,∴∠CMB為二面角B―A1D―A的平面角,
平面A1C1CA中,C1C=CA=2,D為C1C的中點,
∴CG=2,DC=1 在直角三角形CDG中, ,
, .
.
即二面角B―A1D―A的大小為 .……………………8分
.……………………8分
(Ⅲ)取線段AC的中點F,則EF⊥平面A1BD.
證明如下:
∵A1B1C1―ABC為直三棱柱,∴B1C1//BC,
∵由(Ⅰ)BC⊥平面A1C1CA,∴B1C1⊥平面A1C1CA,
∵EF在平面A1C1CA內的射影為C1F,當F為AC的中點時,
C1F⊥A1D,∴EF⊥A1D.
同理可證EF⊥BD,∴EF⊥平面A1BD.……………………12分
19.(解:(1)分別在下表中,填寫隨機變量 和
和 的分布列:
的分布列:
 …4分
…4分
(2) ;
; ;
;


 …………………….. 9分
…………………….. 9分
∴周長 的分布列為:
的分布列為:
 ……….. 10分
……….. 10分
∴ …. 12分
…. 12分
20.(Ⅰ) 設C(x, y),
∵  ,
,  ,
,
∴  ,
,
∴ 由定義知,動點C的軌跡是以A、B為焦點,
長軸長為 的橢圓除去與x軸的兩個交點.
的橢圓除去與x軸的兩個交點.
∴  . ∴
. ∴  .
.
∴ W: 
 . …………………………………………… 2分
. …………………………………………… 2分
(Ⅱ) 設直線l的方程為 ,代入橢圓方程,得
,代入橢圓方程,得 .
.
整理,得 .
①………………………… 5分
.
①………………………… 5分
因為直線l與橢圓有兩個不同的交點P和Q等價于
 ,解得
,解得 或
或 .
.
∴ 滿足條件的k的取值范圍為  ………… 7分
………… 7分
(Ⅲ)設P(x1,y1),Q(x2,y2),則 =(x1+x2,y1+y2),
=(x1+x2,y1+y2),
由①得 .
②
.
②
又 ③
③
因為 ,
, , 所以
, 所以 .……………………… 11分
.……………………… 11分
所以 與
與 共線等價于
共線等價于 .
.
將②③代入上式,解得 .
.
所以存在常數k,使得向量 與
與 共線.…………………… 12分
共線.…………………… 12分
21.解:(1)由題意得
解得 ,將
,將 代入,化簡得
代入,化簡得
 ;………………4分
;………………4分
(2)由題知 ,因為
,因為 ,所以
,所以
令 ,則
,則 ,
,
并且 ,因此
,因此 ,
,
從而 ,得
,得 ,………..8分
,………..8分
(2)因為 時
時 ,故
,故
 ,
,
從而 ………………12分
………………12分
22.解: Ⅰ)∵ =a+
=a+ ,x∈(0,e),
,x∈(0,e), ∈[
∈[ ,+∞
,+∞ ………………1分
………………1分
(1)若a≥- ,則
,則 ≥0,從而f(x)在(0,e)上增函數.
≥0,從而f(x)在(0,e)上增函數.
∴f(x)max =f(e)=ae+1≥0.不合題意. …………………………………3分
(2)若a<- ,則由
,則由 >0
>0 a+
a+ >0,即0<x<-
>0,即0<x<-
由f(x)<0 a+
a+ <0,即-
<0,即- <x≤e.
<x≤e.
∴f(x) =f(-
=f(- )=-1+ln(-
)=-1+ln(- ).
).
令-1+ln(- )=-3,則ln(-
)=-3,則ln(- )=-2.∴-
)=-2.∴- =e
=e ,
,
即a=-e2. ∵-e2<- ,∴a=-e2為所求. ……………………………6分
,∴a=-e2為所求. ……………………………6分
(Ⅱ)當a=-1時,f(x)=-x+lnx, =-1+
=-1+ =
= .
.
當0<x<1時, >0;當x>1時,
>0;當x>1時, <0.
<0.
∴f(x)在(0,1)上是增函數,在(1,+∞)上減函數.
從而f(x) =f(1)=-1.∴f(x)=-x+lnx≤-1,從而lnx≤x-1. ………8分
=f(1)=-1.∴f(x)=-x+lnx≤-1,從而lnx≤x-1. ………8分
令g(x)=|f(x)|- -
- =x-lnx-
=x-lnx- -
- =x-(1+
=x-(1+ )lnx-
)lnx-
(1)當0<x<2時,有g(x)≥x-(1+ )(x-1)-
)(x-1)- =
= -
- >0.
>0.
(2)當x≥2時,g′(x)=1-[(- )lnx+(1+
)lnx+(1+ )?
)? ]=
]=
= .
.
∴g(x)在[2,+∞ 上增函數,
上增函數,
∴g(x)≥g(2)=
綜合(1)、(2)知,當x>0時,g(x)>0,即|f(x)|> .
.
故原方程沒有實解. ……………………………………12分

 其中a∈R
其中a∈R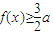 恒成立,求a的取值范圍.
恒成立,求a的取值范圍. 其中a∈R
其中a∈R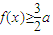 恒成立,求a的取值范圍.
恒成立,求a的取值范圍.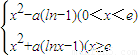 其中a∈R
其中a∈R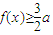 恒成立,求a的取值范圍.
恒成立,求a的取值范圍.