日韩视频―中文字幕,极品女神高潮呻吟av久久,日韩中文字幕一区

已知函數的圖象經過點P(m.n)點.則函數的反函數的圖象必經過點( ) 【查看更多】

題目列表(包括答案和解析)

已知函數f（x）=log₃（ax+b）的圖象經過點A（2，1）和B（5，2），記a_n=3^f（n），n∈N^*
（1）求數列{a_n}的通項公式；
（2）設bn=

，T_n=b₁+b₂+…b_n，若T_n＜m（m∈Z），求m的最小值；
（3）求使不等式(1+

)(1+

)…(1+

)≥p

2n+1

對一切n∈N^*，均成立的最大實數p．

已知函數f(x)＝log₃(ax＋b)的圖象經過點A(2，1)和B(5，2)，記a_n＝3^f(n)，n∈N^*

(Ⅰ)求數列{a_n}的通項公式；

(Ⅱ)設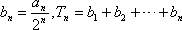，若T_n＜m(m∈Z)，求m的最小值；

(Ⅲ)求使不等式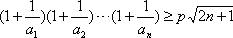對一切n∈N^*均成立的最大實數p．

已知函數f(x)＝log₃(ax＋b)的圖象經過點A(2，1)和B(5，2)，記a_n＝3^f(n)，n∈N*．

(1)求函數f(x)的解析式以及數列{a_n}的通項公式；

(2)求使不等式對一切n∈N^*均成立的最大實數p；

(3)在數列{a_n}中，對每一個k∈N^*，在a_k與a_k+1之間插入2^k－1個2，得到新數列{b_n}，設T_n是數列{b_n}的前n項和，試問是否存在正整數m，使T_m＝2007成立．若存在求出m的值；若不存在，請說明理由．

已知函數f(x)＝ax³＋bx²＋c(a，b，c∈R，a≠0)的圖象經過點P(－1，2)，且在點P處的切線與直線x－3y＝0垂直．

(Ⅰ)若c＝0，試求函數f(x)的單調區間；

(Ⅱ)若a＞0，b＞0，且函數f(x)在區間(－∞，m)及(n，＋∞)上都是增函數，求n－m的取值范圍．

已知二次函數y＝g(x)的圖象經過點O(0，0)、A(m，0)與點P(m＋1，m＋1)，設函數f(x)＝(x－n)g(x)在x＝a和x＝b處取到極值，其中m＞n＞0，b＜a．

(1)求g(x)的二次項系數k的值；

(2)比較a，b，m，n的大小(要求按從小到大排列)；

(3)若m＋n≤2，且過原點存在兩條互相垂直的直線與曲線y＝f(x)均相切，求y＝f(x)．

同步練習冊答案

日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级