
題目列表(包括答案和解析)
 圖中的曲線是
圖中的曲線是![]()
![]() 的圖象,已知
的圖象,已知![]() 的值為
的值為![]() ,
,![]() ,
,![]() ,
,![]() ,則相應(yīng)曲線
,則相應(yīng)曲線![]() 的
的![]() 依次為 ( )
依次為 ( )
A.![]() ,
,![]() ,
,![]() ,
,![]() B.
B.![]() ,
,![]() ,
,![]() ,
,![]()
C.![]() ,
,![]() ,
,![]() ,
,![]() D.
D.![]() ,
,![]() ,
,![]() ,
,![]()
曲線C1、C2、C3、C4分別是指數(shù)函數(shù)y=ax,y=bx,y=cx和y=dx的圖象,則a、b、c、d與1的大小關(guān)系是
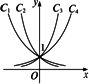
a<b<1<c<d
a<b<1<d<c
b<a<1<c<d
b<a<1<d<c
 圖中曲線是冪函數(shù)y=xn在第一象限的圖像,已知n可取±2,±
圖中曲線是冪函數(shù)y=xn在第一象限的圖像,已知n可取±2,±![]() 四個(gè)值,則相應(yīng)于曲線
四個(gè)值,則相應(yīng)于曲線![]() 的n依次為( )
的n依次為( )
A.-2,-![]() ,
,![]() ,2 B.2,
,2 B.2,![]() ,-
,-![]() ,-2
,-2
C. -![]() ,-2,2,
,-2,2,![]() D. 2,
D. 2,![]() ,-2, -
,-2, -![]()
圖中曲線是冪函數(shù)y=xn在第一象限的圖象,已知n取±3,± 四個(gè)值,則相應(yīng)于曲線C1,C2,C3,C4的n依次為 ( )
四個(gè)值,則相應(yīng)于曲線C1,C2,C3,C4的n依次為 ( )

A.-3,- ,
, ,3 B.3,
,3 B.3, ,-
,- ,-3
,-3
C.- ,-3,3,
,-3,3, D.3,
D.3, ,-3,-
,-3,-
函數(shù)的圖象與方程的曲線有著密切的聯(lián)系,如把拋物線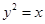 的圖象繞原點(diǎn)沿逆時(shí)針?lè)较蛐D(zhuǎn)
的圖象繞原點(diǎn)沿逆時(shí)針?lè)较蛐D(zhuǎn)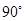 就得到函數(shù)
就得到函數(shù)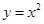 的圖象.若把雙曲線
的圖象.若把雙曲線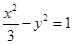 繞原點(diǎn)按逆時(shí)針?lè)较蛐D(zhuǎn)一定角度
繞原點(diǎn)按逆時(shí)針?lè)较蛐D(zhuǎn)一定角度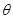 后,能得到某一個(gè)函數(shù)的圖象,則旋轉(zhuǎn)角
后,能得到某一個(gè)函數(shù)的圖象,則旋轉(zhuǎn)角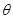 可以是( )
可以是( )
A. B.
B.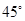 C.
C.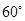 D.
D.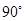
一、選擇題
題號(hào)
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
C
B
A
D
B
C
C
D
D
A
C
二、填空題
13.實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image206.gif) 14.
14.實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image208.gif) 15.4 16.③④
15.4 16.③④
三、解答題
17.解:(1)∵實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image210.gif) ,
,實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image212.gif) ,
,
∴實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image214.gif) .
…………2分
.
…………2分
又實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image216.gif) , …………4分
, …………4分
∴實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image218.gif) ,∴
,∴實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image220.gif) .
…………6分
.
…………6分
(2)∵實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image222.gif) ,
,實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image148.gif) ,
,實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image218.gif) ,
,
∴實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image225.gif) . …………8分
. …………8分
∵實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image227.gif) ,
,
實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image228.gif) ∴
∴實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image230.gif) .
.
∴實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image232.gif) ,
,
∴實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image234.gif) .…………10分
.…………10分
18.(1)證明:連結(jié)BD交AC于點(diǎn)M,取BE的中點(diǎn)N,
連結(jié)MN,則MN∥ED且MN=實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image236.gif) ED,依題意,
ED,依題意,
知AG∥ED且AG=實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image236.gif) ED,
ED,
∴MN∥AG且MN=AG.
故四邊形MNAG是平行四邊形, AM∥GN,
即AC∥GN,…………3分
又∵實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image238.gif)
∴ AC∥平面GBE.…………6分
(2)解:延長(zhǎng)EG交DA的延長(zhǎng)線于H點(diǎn),
連結(jié)BH,作AO⊥GH于O點(diǎn),連結(jié)BO.
∵ 平面ABCD⊥平面ADEF,平面ABCD∩平面ADEF=AD ,AB⊥AD
∴ AB⊥平面ADEF,由三垂線定理,知AB⊥GH,
故∠AOB就是二面角B-GE-D的平面角.…………8分
∵ 平面ABCD⊥平面ADEF,平面ABCD∩平面ADEF=AD ,ED⊥AD
∴ ED⊥平面ABCD,
故∠EBD就是直線BE與平面ABCD成的角,……10分
知∠EBD=45°,設(shè)AB=a,則BE=BD=實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image240.gif) a.
a.
在直角三角形AGH中:AH=AD= a,AG=實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image242.gif) =
=實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image244.gif) a,
a,
HG=實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image246.gif) ,AO=
,AO=實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image248.gif) .
.
在直角三角形ABO中:tan∠AOB=實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image250.gif) .
.
∴ ∠AOB=60°.
故二面角B-GE-D的大小為60°.…………12分
19.解:(1)記A0表示事件“取出的2件產(chǎn)品中無(wú)二等品”,A1表示事件“取出的2件產(chǎn)品中恰有1件是二等品”.則A0、A1互斥,且A=A0+A1.
故P (A)=P (A0+A1)=P
(A0) +P (A1)=(1-p)2+C實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image252.gif) p (1-p)=1-p2.
p (1-p)=1-p2.
依題意,知1-p2=0.96,又p>0,得p=0.2.…………6分
(2)(理)ξ可能的取值為0,1,2.
若該批產(chǎn)品共100件,由(1)知,其中共有二等品100×0.2=20件,故
P(ξ=0)=實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image254.gif) .P(ξ=1)=
.P(ξ=1)=實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image256.gif) .
.
P(ξ=2)=實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image258.gif) .…………9分
.…………9分
所以ξ的分布列為
ξ
0
1
2
P
實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image260.gif)
實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image262.gif)
實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image264.gif)
實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image266.gif) ξ的期望
ξ的期望實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image268.gif) …………12分
…………12分
20.解 (1)實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image270.gif) 在
在實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image272.gif) 上單調(diào)遞增,
上單調(diào)遞增,實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image274.gif) 上單調(diào)遞減,
上單調(diào)遞減,
實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image276.gif) 有兩根
有兩根實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image278.gif) ,
,
實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image280.gif) ……4分
……4分
令實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image282.gif) ,
,
則實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image284.gif) ,
,
因?yàn)?sub>實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image286.gif) 在
在實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image288.gif) 上恒大于0,所以
上恒大于0,所以實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image290.gif) 在
在實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image288.gif) 上單調(diào)遞增,
上單調(diào)遞增,
故實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image292.gif) ,
, 實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image294.gif) ,
,
實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image296.gif) .
……………6分
.
……………6分
(2)實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image298.gif) ,
,
實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image300.gif) .
.
實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image302.gif) .
………………8分
.
………………8分
①當(dāng)實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image304.gif) 時(shí),
時(shí),實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image306.gif) ,定義域?yàn)?sub>
,定義域?yàn)?sub>實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image308.gif) ,
,
實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image310.gif) 恒成立,
恒成立,實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image312.gif) 上單調(diào)遞增;
…………9分
上單調(diào)遞增;
…………9分
②當(dāng)實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image314.gif) 時(shí),
時(shí),實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image316.gif) ,定義域:
,定義域:實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image318.gif) ,
,
實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image310.gif) 恒成立,
恒成立,實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image321.gif) 上單調(diào)遞增; …………10分
上單調(diào)遞增; …………10分
③當(dāng)實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image323.gif) 時(shí),
時(shí),實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image325.gif) ,定義域:
,定義域:實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image318.gif) ,
,
由實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image310.gif) 得
得實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image327.gif) ,由
,由實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image329.gif) 得
得實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image331.gif) .
.
故在實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image333.gif) 上單調(diào)遞增;在
上單調(diào)遞增;在實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image335.gif) 上單調(diào)遞減. …………11分
上單調(diào)遞減. …………11分
所以當(dāng)實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image304.gif) 時(shí),
時(shí),實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image312.gif) 上單調(diào)遞增,故
上單調(diào)遞增,故實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image337.gif) 無(wú)極值;
無(wú)極值;
當(dāng)實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image314.gif) 時(shí),
時(shí),實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image321.gif) 上單增;故
上單增;故實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image337.gif) 無(wú)極值.
無(wú)極值.
當(dāng)實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image323.gif) 時(shí),
時(shí),實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image337.gif) 在
在實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image333.gif) 上單調(diào)遞增;在
上單調(diào)遞增;在實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image335.gif) 上單調(diào)遞減.
上單調(diào)遞減.
故實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image337.gif) 有極小值,且
有極小值,且實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image337.gif) 的極小值為
的極小值為實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image341.gif) . …12分
. …12分
21.解:(I)設(shè)實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image343.gif) 依題意得
依題意得
實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image345.gif) …………2分
…………2分
消去實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image347.gif) ,整理得
,整理得實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image349.gif) .…………4分
.…………4分
當(dāng)實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image351.gif) 時(shí),方程表示焦點(diǎn)在
時(shí),方程表示焦點(diǎn)在實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image353.gif) 軸上的橢圓;
軸上的橢圓;
當(dāng)實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image355.gif) 時(shí),方程表示焦點(diǎn)在
時(shí),方程表示焦點(diǎn)在實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image357.gif) 軸上的橢圓;
軸上的橢圓;
當(dāng)實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image359.gif) 時(shí),方程表示圓. …………6分
時(shí),方程表示圓. …………6分
(II)當(dāng)實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image361.gif) 時(shí),方程為
時(shí),方程為實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image363.gif) ,
,
設(shè)直線實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image093.gif) 的方程為
的方程為實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image366.gif) ,
,
實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image368.gif) …………8分
…………8分
消去實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image353.gif) 得
得實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image371.gif) .…………10分
.…………10分
根據(jù)已知可得實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image373.gif) ,故有
,故有實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image375.gif) ,
,
實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image377.gif) ,
,
實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image266.gif) 直線
直線實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image093.gif) 的斜率為
的斜率為實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image381.gif) . …………12分
. …………12分
22.證明 (Ⅰ)即證實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image383.gif) .
.
實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image385.gif)
實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image387.gif) ,
,實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image389.gif) ,
,實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image391.gif) ,
,
實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image266.gif)
實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image394.gif) .…………2分
.…………2分
假設(shè)實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image396.gif) ,則
,則
實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image398.gif) ,…………4分
,…………4分
實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image400.gif) ,
,
實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image266.gif)
實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image403.gif) .
.
綜上所述,根據(jù)數(shù)學(xué)歸納法,命題成立. …………6分
(Ⅱ)由(Ⅰ),得
實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image405.gif) ,…………8
,…………8
實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image266.gif)
實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image408.gif) .…………10
.…………10
又 實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image410.gif) ,
,實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image266.gif)
實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image413.gif) ,
,
即實(shí)驗(yàn)中學(xué)2009年高三數(shù)學(xué)第二次質(zhì)量檢測(cè)(理科).files/image415.gif) .………12分
.………12分
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com