
題目列表(包括答案和解析)
設(shè)![]() 上的兩個函數(shù),若對任意的
上的兩個函數(shù),若對任意的![]() ,都有
,都有![]() 上是“密切函數(shù)”,[a,b]稱為“密切區(qū)間”,設(shè)
上是“密切函數(shù)”,[a,b]稱為“密切區(qū)間”,設(shè)![]() 上是“密切函數(shù)”,則它的“密切區(qū)間”可以是 ( )
上是“密切函數(shù)”,則它的“密切區(qū)間”可以是 ( )
設(shè)![]() 上的兩個函數(shù),若對任意的
上的兩個函數(shù),若對任意的![]() ,都有
,都有![]() 上是“接近函數(shù)”,[a,b]稱為“接近區(qū)間”,設(shè)
上是“接近函數(shù)”,[a,b]稱為“接近區(qū)間”,設(shè)
f(x)= x2–4x ,g(x)= x-7在[a,b]上是“接近函數(shù)”,則它的“接近區(qū)間”可以是 A.[2,3] B.[1,4] C.[3,4] D.[2,4]
設(shè)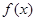 與
與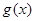 是定義在同一區(qū)間
是定義在同一區(qū)間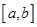 上的兩個函數(shù),若對任意的
上的兩個函數(shù),若對任意的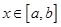 ,
,
都有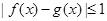 ,則稱
,則稱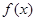 和
和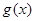 在
在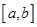 上是“密切函數(shù)”,
上是“密切函數(shù)”,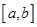 稱為“密切區(qū)
稱為“密切區(qū)
間”,設(shè)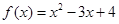 與
與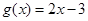 在
在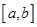 上是“密切函數(shù)”,則它的“密切區(qū)間”
上是“密切函數(shù)”,則它的“密切區(qū)間”
可以是 ( )
A.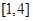 B.
B. 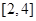 C.
C. 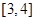 D.
D. 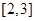
設(shè)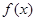 和
和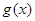 是定義在同一區(qū)間
是定義在同一區(qū)間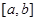 上的兩個函數(shù),若對任意的
上的兩個函數(shù),若對任意的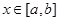 ,都有
,都有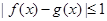 ,則稱
,則稱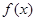 和
和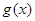 在
在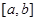 上是“密切函數(shù)”,
上是“密切函數(shù)”,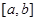 稱為“密切區(qū)間”,設(shè)
稱為“密切區(qū)間”,設(shè)
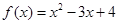 與
與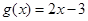 在
在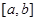 上是“密切函數(shù)”,則它的“密切區(qū)間”可以是 ( )
上是“密切函數(shù)”,則它的“密切區(qū)間”可以是 ( )
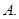
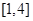
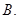
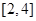
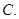
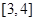
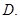
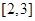
設(shè)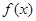 與
與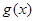 是定義在同一區(qū)間
是定義在同一區(qū)間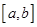 上的兩個函數(shù),若對任意的
上的兩個函數(shù),若對任意的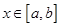 ,都有
,都有 ,則稱
,則稱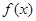 和
和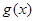 在
在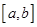 上 是“密切函數(shù)”,
上 是“密切函數(shù)”,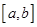 稱為“密切區(qū)間”,設(shè)
稱為“密切區(qū)間”,設(shè)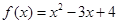 與
與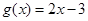 在
在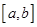 上是“密切函數(shù)”,則它的“密切區(qū)間”可以是 ( )
上是“密切函數(shù)”,則它的“密切區(qū)間”可以是 ( )
A.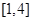 | B.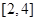 | C.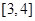 | D. |
第Ⅰ卷(選擇題,共50分)
1―3 AAD 4(文)D(理)B 5(文)B(理)C
|