1.3.5
第Ⅱ卷(非選擇題,共100分)
二、填空題
11.4 12.96 13.-3 14.(文).files/image182.gif) (理)
(理).files/image184.gif)
15.(文).files/image186.gif) (理)
(理).files/image188.gif)
三、解答題
16.解:(1).files/image190.gif)
.files/image192.gif)
.files/image194.gif)
.files/image196.gif)
.files/image198.gif)
.files/image200.gif) …………(4分)
…………(4分)
(1)(文科)在.files/image202.gif) 時,
時,
.files/image204.gif)
.files/image206.gif)
在.files/image208.gif) 時,
時,.files/image044.gif) 為減函數
為減函數
從而.files/image044.gif) 的單調遞減區間為
的單調遞減區間為.files/image210.gif) ;…………(文8分)
;…………(文8分)
(2)(理科).files/image204.gif)
.files/image206.gif)
當.files/image202.gif) 時,由
時,由.files/image208.gif) 得單調遞減區間為
得單調遞減區間為.files/image210.gif)
同理,當.files/image213.gif) 時,函數的單調遞減區間為
時,函數的單調遞減區間為.files/image215.gif) …………(理8分)
…………(理8分)
(3)當.files/image217.gif) ,變換過程如下:
,變換過程如下:
1°將.files/image219.gif) 的圖象向右平移
的圖象向右平移.files/image221.gif) 個單位可得函數
個單位可得函數.files/image223.gif) 的圖象。
的圖象。
2°將所得函數圖象上每個點的縱坐標擴大為原來的.files/image225.gif) 倍,而橫坐標保持不變,可得函數
倍,而橫坐標保持不變,可得函數.files/image227.gif) 的圖象。
的圖象。
3°再將所得圖象向上平移一個單位,可得.files/image229.gif) 的圖象……(12分)
的圖象……(12分)
(其它的變換方法正確相應給分)
17.解:(1).files/image231.gif) 三棱柱ABC―A1B1C1為直三棱柱
三棱柱ABC―A1B1C1為直三棱柱
.files/image233.gif) 底面ABC
底面ABC
又.files/image231.gif) AC
AC.files/image235.gif) 面ABC
面ABC
.files/image233.gif) AC
AC
又.files/image238.gif)
.files/image240.gif)
又.files/image231.gif) AC
AC.files/image235.gif) 面B1AC
面B1AC
.files/image242.gif) …………(6分)
…………(6分)
(2).files/image231.gif) 三棱柱ABC―A1B1C1為直三棱柱
三棱柱ABC―A1B1C1為直三棱柱
.files/image244.gif) 底面ABC
底面ABC
.files/image246.gif) 為直線B1C與平面ABC所成的角,即
為直線B1C與平面ABC所成的角,即.files/image248.gif)
過點A作AM⊥BC于M,過M作MN⊥B1C于N,加結AN。
∴平面BB1CC1⊥平面ABC
∴AM⊥平面BB1C1C
由三垂線定理知AN⊥B1C從而∠ANM為二面角B―B1C―A的平面角。
設AB=BB1=.files/image250.gif)
在Rt△B1BC中,BC=BB1.files/image252.gif)
.files/image254.jpg)
即二面角B―B1C―A的正切值為.files/image256.gif) …………(文12分)
…………(文12分)
(3)(理科)過點A1作A1H⊥平面B1AC于H,連結HC,則
∠A1CH為直線A1C與平面B1AC所成的角
由.files/image258.gif) 知
知
.files/image260.gif)
在Rt.files/image262.gif) ………………(理12分)
………………(理12分)
18.解:(文科)(1)從口袋A中摸出的3個球為最佳摸球組合即為從口袋A中摸出2個紅球和1個黑球,其概率為
.files/image264.gif) ………………………………(6分)
………………………………(6分)
(2)由題意知:每個口袋中摸球為最佳組合的概率相同,從5個口袋中摸球可以看成5次獨立重復試難,故所求概率為
.files/image266.gif) ……………………………………(12分)
……………………………………(12分)
(理科)(1)設用隊獲第一且丙隊獲第二為事件A,則
.files/image268.gif) ………………………………………(6分)
………………………………………(6分)
(2).files/image270.gif) 可能的取值為0,3,6;則
可能的取值為0,3,6;則
甲兩場皆輸:.files/image272.gif)
甲兩場只勝一場:.files/image274.gif)

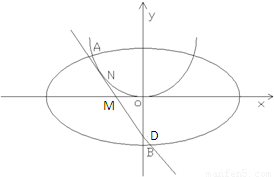
 橢圓E:
橢圓E: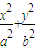 =1(a>b>0)離心率為
=1(a>b>0)離心率為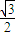 ,且過P(
,且過P(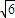 ,
,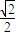 ).
). ,0),且與開口朝上,頂點在原點的拋物線C切于第二象限的一點N,直 線l與橢圓E交于A,B兩點,與y軸交與D點,若
,0),且與開口朝上,頂點在原點的拋物線C切于第二象限的一點N,直 線l與橢圓E交于A,B兩點,與y軸交與D點,若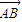 =
=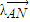 ,
,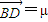
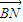 ,且λ+μ=
,且λ+μ= ,求拋物線C的標準方程.
,求拋物線C的標準方程.