
題目列表(包括答案和解析)
已知函數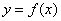 的定義域為
的定義域為 ,當
,當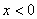 時,
時,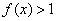 ,且對任意的
,且對任意的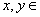
 ,等式
,等式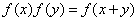 成立.若數列
成立.若數列 滿足
滿足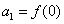 ,且
,且
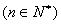 ,則
,則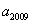 的值為 ( )A.
4016 B. 4017 C. 4018 D. 4019
的值為 ( )A.
4016 B. 4017 C. 4018 D. 4019
{an}是等差數列,a1>0,a2009+a2010>0,a2009?a2010<0,使前n項和Sn>0成立的最大自然數n是
A.4019 B.
已知函數 的定義域為
的定義域為 ,當
,當 時,
時, ,且對任意的
,且對任意的 ,等式
,等式 成立,若數列
成立,若數列 滿足
滿足 ,且
,且 則
則 的值為( )
的值為( )
| A.4016 | B.4017 | C.4018 | D.4019 |
 是定義在R上的單調函數,且對任意
是定義在R上的單調函數,且對任意 都有
都有 成立;若數列
成立;若數列 滿足
滿足 且
且 (n∈
(n∈ ),則
),則 的值為
的值為[ ]
一、選擇題(本大題共12小題,每題5分,共60分)
1.A 2.B 3.C 4.A 5.D 6.C 7.B 8.C 9.A
10.B 11.(理)C(文)B 12.D
二、填空題(本大題共4小題,每題4分,共16分)
13..files/image132.gif) 14.②③ 15.47 16.□
14.②③ 15.47 16.□
三、解答題(本大題共6小題,共計76分)
17.解:(1)依題意函數.files/image110.gif) 的圖象按向量
的圖象按向量.files/image134.gif) 平移后得
平移后得
.files/image048.gif)
.files/image136.gif) ………………………2分
………………………2分
即.files/image048.gif) =
=.files/image138.gif) ………………………4分
………………………4分
又.files/image140.gif)
比較得a=1,b=0 ………………………6分
(2).files/image142.gif)
=.files/image144.gif) ………………………9分
………………………9分
.files/image146.gif)
.files/image148.gif)
∴.files/image104.gif) 的單調增區間為[
的單調增區間為[.files/image151.gif) ,
,.files/image153.gif) ]
].files/image155.gif) ……………………12分
……………………12分
18.解:
(1)設連對的個數為y,得分為x
因為y=0,1,2,4,所以x=0,2,4,8.
.files/image157.gif)
|