……9分
(2)Ex=0×.files/image159.gif) +2×
+2×.files/image009.gif) +4×
+4×.files/image162.gif) +8×
+8×.files/image164.gif) =2
=2
即該人得分的期望為2分。 ……………………12分
(文)
(1)從口袋A中摸出的3個球為最佳摸球組合即為從口袋A中摸出2個紅球和一個黑球
其概念為.files/image168.gif) ……………………6分
……………………6分
(2)由題意知:每個口袋中摸球為最佳組合的概率相同,從5個口袋中摸球可以看成5
次獨立重復試驗,故所求概率為.files/image170.gif) ………………………12分
………………………12分
.files/image172.jpg) 19.解法一:以D為原點,DA,DC,DD1
19.解法一:以D為原點,DA,DC,DD1
所在直線分別為x軸、y軸、z軸,建
立空間直角坐標系D―xyz,則
A(a,0,0)、B(a,2a,0)、
C(0,2a,0)、A1(a,0,a)、
D1(0,0,a)。E、P分別是BC、A1D1
的中點,M、N分別是AE、CD1的中點
∴.files/image174.gif) ……………………………………2分
……………………………………2分
(1).files/image176.gif) ⊥面ADD1A1
⊥面ADD1A1
而.files/image178.gif) =0,∴
=0,∴.files/image180.gif) ⊥
⊥.files/image182.gif) ,又∵MN
,又∵MN.files/image184.gif) 面ADD1A1,∴MN∥面ADD1A1;………4分
面ADD1A1,∴MN∥面ADD1A1;………4分
(2)設面PAE的法向量為.files/image186.gif) ,又
,又.files/image188.gif)
則又.files/image190.gif)
∴.files/image192.gif) =(4,1,2),又你ABCD的一個法向量為
=(4,1,2),又你ABCD的一個法向量為.files/image194.gif) =(0,0,1)
=(0,0,1)
∴.files/image196.gif)
所以二面角P―AE―D的大小為.files/image198.gif) ………………………8分
………………………8分
(3)設.files/image200.gif) 為平面DEN的法向量
為平面DEN的法向量.files/image202.gif) ⊥
⊥.files/image204.gif) ,
,.files/image202.gif) ⊥
⊥.files/image206.gif)
又.files/image204.gif) =(
=(.files/image208.gif) ),
),.files/image206.gif) =(0,a,
=(0,a,.files/image210.gif) ),
),.files/image212.gif) (
(.files/image210.gif) ,0,a)
,0,a)
∴.files/image214.gif) 所以面DEN的一個法向量
所以面DEN的一個法向量.files/image202.gif) =(4,-1,2)
=(4,-1,2)
∵P點到平面DEN的距離為.files/image216.gif)
∴.files/image218.gif)
.files/image220.gif)
所以.files/image222.gif) ……………………12分
……………………12分
解法二:
(1)證明:取CD的中點為K,連接
∵M,N,K分別為AE,CD1,CD的中點
∴MK∥AD,ND∥DD1,∴MK∥面ADD1A1,NK∥面ADD1A1
∴面MNK∥面ADD1A1,∴MN∥面ADD1A1, ………………………4分
(2)設F為AD的中點,∵P為A1D1的中點
.files/image224.jpg) ∴PF∥DD1,PF⊥面ABCD
∴PF∥DD1,PF⊥面ABCD
作FH⊥AE,交AE于H,連結PH,則由三垂
線定理得AE⊥PH,從而∠PHF為二面角
P―AE―D的平面角。
在Rt△AAEF中,AF=.files/image210.gif) ,EF=2
,EF=2.files/image227.gif) ,AE=
,AE=.files/image229.gif) ,
,
從而FH=.files/image231.gif)
在Rt△PFH中,tan∠PHF=.files/image233.gif)
故:二面角P―AE―D的大小為arctan.files/image235.gif)
(3).files/image237.gif)
作DQ⊥CD1,交CD1于Q,
由A1D1⊥面CDD1C1,得A1D1⊥DQ,∴DQ⊥面BCD1A1。
在Rt△CDD1中,.files/image239.gif)
∴.files/image241.gif) ……………………12分
……………………12分
20.解:(理)
(1)函數.files/image048.gif) 的定義域為(0,+
的定義域為(0,+.files/image244.gif) )
)
當a=-2e時,.files/image246.gif) ……………………2分
……………………2分
當x變化時,.files/image248.gif) ,
,.files/image048.gif) 的變化情況如下:
的變化情況如下:
.files/image250.gif)
(0,.files/image252.gif) )
)
.files/image252.gif)
(.files/image252.gif) ,+
,+.files/image244.gif) )
)
.files/image248.gif)
―
0
+
.files/image048.gif)
ㄋ
極小值
ㄊ
由上表可知,函數.files/image048.gif) 的單調遞減區間為(0,
的單調遞減區間為(0,.files/image252.gif) )
)
單調遞增區間為(.files/image252.gif) ,+
,+.files/image244.gif) )
)
極小值是.files/image256.gif) (
(.files/image252.gif) )=0 ……………………6分
)=0 ……………………6分
(2)由.files/image258.gif) ……………………7分
……………………7分
又函數.files/image260.gif) 為[1,4]上單調減函數,
為[1,4]上單調減函數,
則.files/image262.gif) 在[1,4]上恒成立,所以不等式
在[1,4]上恒成立,所以不等式.files/image264.gif) 在[1,4]上恒成立。
在[1,4]上恒成立。
即.files/image266.gif) 在,[1,4]上恒成立 ……………………10分
在,[1,4]上恒成立 ……………………10分
又.files/image268.gif) =
=.files/image270.gif) 在[1,4]上為減函數
在[1,4]上為減函數
∴.files/image268.gif) 的最小值為
的最小值為.files/image273.gif)
∴.files/image275.gif)
.files/image277.gif) ……………………12分
……………………12分
(文)(1)∵函數.files/image279.gif) 在[0,1]上單調遞增,在區間
在[0,1]上單調遞增,在區間.files/image116.gif) 上單調遞減,
上單調遞減,
∴x=1時,取得極大值,
∴.files/image282.gif)
∴4-12+2a=0.files/image284.gif) a=4 ………………………4分
a=4 ………………………4分
(2)A(x0,f(x0))關于直線x=1的對稱點B的坐標為(2-
x0,f(x0)
.files/image286.gif)
=.files/image288.gif)
∴A關于直線x=1的對稱點B也在函數.files/image048.gif) 的圖象上 …………………8分
的圖象上 …………………8分
(3)函數.files/image118.gif) 的圖象與函數
的圖象與函數.files/image048.gif) 的圖象恰有3個交點,等價于方程
的圖象恰有3個交點,等價于方程
.files/image292.gif) 恰有3個不等實根,
恰有3個不等實根,
.files/image294.gif)
∵x=0是其中一個根,
∴方程.files/image296.gif) 有兩個非零不等實根
有兩個非零不等實根
.files/image298.gif) ……………………12分
……………………12分
21.解:(理)(1)由已知得:
.files/image300.gif)
.files/image302.gif)
∵.files/image304.gif) ①…………………2分
①…………………2分
∴.files/image306.gif) ②
②
②―①.files/image308.gif)
即.files/image310.gif)
又.files/image312.gif)
∴.files/image314.gif) ……………………5分
……………………5分
∴{an}成等差數列,且d=1,又a1=1,∴.files/image316.gif) …………………6分
…………………6分
(2)∵.files/image318.gif)
∴.files/image320.gif)
∴.files/image322.gif) …………………8分
…………………8分
兩式相減
.files/image324.gif)
∴.files/image326.gif) ……………………10分
……………………10分
∴.files/image328.gif) ……………………12分
……………………12分
(文)(1)由已知得:
.files/image300.gif)
∴.files/image331.gif)
∵.files/image333.gif) ①…………………2分
①…………………2分
∴.files/image306.gif) ②
②
②―①.files/image308.gif)
即.files/image310.gif)
又.files/image312.gif)
∴.files/image314.gif) ……………………5分
……………………5分
∴{an}成等差數列,且d=1,又a1=1,∴.files/image316.gif) …………………6分
…………………6分
(2)∵.files/image318.gif)
∴.files/image320.gif)
∴.files/image322.gif) …………………8分
…………………8分
兩式相減
.files/image324.gif)
∴.files/image326.gif) ……………………10分
……………………10分
∴.files/image328.gif) ……………………12分
……………………12分
22.解:(1)
設M(x,y)是曲線C上任一點,因為PM⊥x軸,.files/image126.gif)
所以點P的坐標為(x,3y) …………………2分
點P在橢圓.files/image124.gif) ,所以
,所以.files/image338.gif)
因此曲線C的方程是.files/image340.gif) …………………5分
…………………5分
(2)當直線l的斜率不存在時,顯然不滿足條件
所以設直線l的方程為.files/image342.gif) 與橢圓交于A(x1,y1),B(x2,y2),N點所在直線方
與橢圓交于A(x1,y1),B(x2,y2),N點所在直線方
程為
.files/image344.gif) ,由
,由.files/image346.gif) 得
得.files/image348.gif)
.files/image350.gif) ……………………6分
……………………6分
由△=.files/image352.gif) ………………8分
………………8分
∵.files/image354.gif) ,所以四邊形OANB為平行四邊形 …………………9分
,所以四邊形OANB為平行四邊形 …………………9分
假設存在矩形OANB,則.files/image356.gif)
.files/image358.gif)
.files/image360.gif)
所以.files/image362.gif)
即.files/image364.gif) ……………………11分
……………………11分
設N(.files/image366.gif) ),由
),由.files/image354.gif) ,得
,得
.files/image368.gif) ,
,
即N點在直線.files/image344.gif)
所以存在四邊形OANB為矩形,直線l的方程為.files/image371.gif) ……………………14分
……………………14分

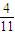
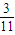
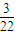
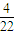
.files/image132.gif) 14.②③ 15.47 16.□
14.②③ 15.47 16.□.files/image110.gif) 的圖象按向量
的圖象按向量.files/image134.gif) 平移后得
平移后得.files/image048.gif)
.files/image136.gif) ………………………2分
………………………2分.files/image048.gif) =
=.files/image138.gif) ………………………4分
………………………4分.files/image140.gif)
.files/image142.gif)
.files/image144.gif) ………………………9分
………………………9分.files/image146.gif)
.files/image148.gif)
.files/image104.gif) 的單調增區間為[
的單調增區間為[.files/image151.gif) ,
,.files/image153.gif) ]
].files/image155.gif) ……………………12分
……………………12分.files/image157.gif)