
題目列表(包括答案和解析)
. (本題滿分16分,第1小題滿分4分,第2小題滿分6分,第3小題滿分6分)
已知公差大于零的等差數列 的前
的前 項和為
項和為 ,且滿足
,且滿足 ,
, ,
,
(1)求數列 的通項公式;
的通項公式;
(2)若數列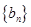 是等差數列,且
是等差數列,且 ,求非零常數
,求非零常數 ;
;
(3)若(2)中的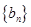 的前
的前 項和為
項和為 ,求證:
,求證: .
.
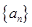 的前
的前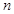 項和為
項和為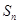 ,且滿足
,且滿足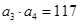 ,
,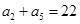 ,
,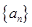 的通項公式;
的通項公式;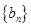 是等差數列,且
是等差數列,且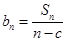 ,求非零常數
,求非零常數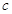 ;
;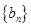 的前
的前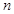 項和為
項和為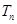 ,求證:
,求證: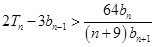 .
.(本題滿分16分,第1小題4分,第2小題6分,第3小題6分)
設橢圓的中心為原點O,長軸在x軸上,上頂點為A,左、右焦點分別為F1、F2,線段OF1、OF2的中點分別為B1、B2,且△AB1B2是面積為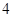 的直角三角形.過B1作直線l交橢圓于P、Q兩點.
的直角三角形.過B1作直線l交橢圓于P、Q兩點.
(1) 求該橢圓的標準方程;
(2) 若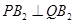 ,求直線l的方程;
,求直線l的方程;
(3) 設直線l與圓O:x2+y2=8相交于M、N兩點,令|MN|的長度為t,若t∈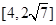 ,求△B2PQ的面積
,求△B2PQ的面積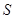 的取值范圍.
的取值范圍.
(本題滿分16分,第1小題4分,第2小題6分,第3小題6分)
設橢圓的中心為原點O,長軸在x軸上,上頂點為A,左、右焦點分別為F1、F2,線段OF1、OF2的中點分別為B1、B2,且△AB1B2是面積為 的直角三角形.過B1作直線l交橢圓于P、Q兩點.
的直角三角形.過B1作直線l交橢圓于P、Q兩點.
(1) 求該橢圓的標準方程;
(2) 若 ,求直線l的方程;
,求直線l的方程;
(3) 設直線l與圓O:x2+y2=8相交于M、N兩點,令|MN|的長度為t,若t∈ ,求△B2PQ的面積
,求△B2PQ的面積 的取值范圍.
的取值范圍.
(本題滿分16分,第1小題 4分,第2小題4分,第3小題8分)
已知函數![]() 在點
在點![]() 處的切線方程為
處的切線方程為![]() .
.
⑴求函數![]() 的解析式;
的解析式;
⑵若對于區間![]() 上任意兩個自變量的值
上任意兩個自變量的值![]() 都有
都有![]() ,求實數
,求實數![]() 的最小值;
的最小值;
⑶若過點![]() 可作曲線
可作曲線![]() 的三條切線,求實數
的三條切線,求實數![]() 的取值范圍.
的取值范圍.
一、填空題(本大題滿分48分,每小題4分)
(1)3 (2)(5,0) (3){1,2,5} (4)2 (5)(-2,0)∪(2,5]
(6)(5,4) (7)6 (8)(x-2)2+(y+3)2=5 (9)(文史類).files\image052.png) (10)a>0且b≤0
(10)a>0且b≤0
(11)用代數的方法研究圖形的幾何性質 (12)①、④
二、選擇題(本大題滿分16分,每小題4分)
(13)B (14)C (15)A (16)B
三、解答題(本大題滿分86分)
(17)【解】由題意得 z1=(文史類).files\image054.png) =2+3i,
=2+3i,
于是(文史類).files\image027.png) =
=(文史類).files\image056.png) =
=(文史類).files\image058.png) ,
,(文史類).files\image029.png) =
=(文史類).files\image061.png) .
.
(文史類).files\image058.png) <
<(文史類).files\image061.png) ,得a2-8a+7<0,1<a<7.
,得a2-8a+7<0,1<a<7.
(18)【解】由題意得xy+(文史類).files\image063.png) x2=8, ∴y=
x2=8, ∴y=(文史類).files\image065.png) =
=(文史類).files\image067.png) (0<x<4
(0<x<4(文史類).files\image069.png) ).
).
于定, 框架用料長度為
l=2x+2y+2((文史類).files\image071.png) )=(
)=((文史類).files\image073.png) +
+(文史類).files\image069.png) )x+
)x+(文史類).files\image076.png) ≥4
≥4(文史類).files\image078.png) .
.
當((文史類).files\image073.png) +
+(文史類).files\image069.png) )x=
)x=(文史類).files\image076.png) ,即x=8-4
,即x=8-4(文史類).files\image069.png) 時等號成立.
時等號成立.
此時, x≈2.343,y=2(文史類).files\image069.png) ≈2.828. 故當x為2.343m,y為2.828m時, 用料最省.
≈2.828. 故當x為2.343m,y為2.828m時, 用料最省.
(19)【解】(1)2-(文史類).files\image081.png) ≥0, 得
≥0, 得(文史類).files\image083.png) ≥0, x<-1或x≥1
即A=(-∞,-1)∪[1,+ ∞)
≥0, x<-1或x≥1
即A=(-∞,-1)∪[1,+ ∞)
(2)
由(x-a-1)(
∵a<1,∴a+1>
∵B(文史類).files\image034.png) A, ∴2 a≥1或a +1≤-1, 即a≥
A, ∴2 a≥1或a +1≤-1, 即a≥(文史類).files\image002.png) 或a≤-2, 而a <1,
或a≤-2, 而a <1,
∴(文史類).files\image002.png) ≤a <1或a≤-2, 故當B
≤a <1或a≤-2, 故當B(文史類).files\image034.png) A時, 實數a的取值范圍是 (-∞,-2)∪[
A時, 實數a的取值范圍是 (-∞,-2)∪[(文史類).files\image002.png) ,1]
,1]
(文史類).files\image084.png)
(文史類).files\image085.png)
(文史類).files\image086.png) (20)【解】(1) 解方程 y=
(20)【解】(1) 解方程 y=(文史類).files\image002.png) x 得 x1=-4, x2=8
x 得 x1=-4, x2=8
y=(文史類).files\image037.png) x2-4 y1=-2, y2=4
x2-4 y1=-2, y2=4
即A(-4,-2),B(8,4), 從而AB的中點為M(2,1).
由kAB==(文史類).files\image002.png) ,直線AB的垂直平分線方程y-1=
,直線AB的垂直平分線方程y-1=(文史類).files\image002.png) (x-2).
(x-2).
令y=-5, 得x=5, ∴Q(5,-5)
(2)
直線OQ的方程為x+y=0, 設P(x, (文史類).files\image037.png) x2-4).
x2-4).
∵點P到直線OQ的距離d=(文史類).files\image088.png) =
=(文史類).files\image090.png) ,
,
(文史類).files\image092.png) ,∴SΔOPQ=
,∴SΔOPQ=(文史類).files\image002.png)
(文史類).files\image094.png) =
=(文史類).files\image096.png) .
.
∵P為拋物線上位于線段AB下方的點, 且P不在直線OQ上,
∴-4≤x<4(文史類).files\image098.png) -4或4
-4或4(文史類).files\image098.png) -4<x≤8. ∵函數y=x2+8x-32在區間[-4,8] 上單調遞增,
-4<x≤8. ∵函數y=x2+8x-32在區間[-4,8] 上單調遞增,
∴當x=8時, ΔOPQ的面積取到最大值30.
(21)【證明】(1) ∵棱臺DEF―ABC與棱錐P―ABC的棱長和相等,
∴DE+EF+FD=PD+OE+PF. 又∵截面DEF∥底面ABC,
∴DE=EF=FD=PD=OE=PF,∠DPE=∠EPF=∠FPD=60°, ∴P―ABC是正四面體.
【解】(2)取BC的中點M,連拉PM,DM.AM.
∵BC⊥PM,BC⊥AM, ∴BC⊥平面PAM,BC⊥DM,
則∠DMA為二面角D―BC―A的平面角. 由(1)知,P―ABC的各棱長均為1,
∴PM=AM=(文史類).files\image100.png) ,由D是PA的中點, 得sin∠DMA=
,由D是PA的中點, 得sin∠DMA=(文史類).files\image102.png) ,∴∠DMA=arcsin
,∴∠DMA=arcsin(文史類).files\image104.png) .
.
(3)存在滿足條件的直平行六面體. 棱臺DEF―ABC的棱長和為定值6,體積為V.
設直平行六面體的棱長均為(文史類).files\image002.png) ,底面相鄰兩邊夾角為α,
,底面相鄰兩邊夾角為α,
則該六面體棱長和為6, 體積為(文史類).files\image037.png) sinα=V.
sinα=V.
∵正四面體P―ABC的體積是(文史類).files\image107.png) ,∴0<V<
,∴0<V<(文史類).files\image107.png) ,0<8V<1.可知α=arcsim(8V)
,0<8V<1.可知α=arcsim(8V)
故構造棱長均為(文史類).files\image002.png) ,底面相鄰兩邊夾角為arcsim(8V)的直平行六面體即滿足要求.
,底面相鄰兩邊夾角為arcsim(8V)的直平行六面體即滿足要求.
(22)【解】(1) a1=(文史類).files\image041.png) 2=9,由S3=
2=9,由S3=(文史類).files\image073.png) (a1+a3)=162,得a3=
(a1+a3)=162,得a3=(文史類).files\image110.png) 3=99.
3=99.
由
(文史類).files\image111.png)
(文史類).files\image047.png) -y2=1
-y2=1
,得
(文史類).files\image112.png) x
x(文史類).files\image114.png) =90
=90
x(文史類).files\image114.png) +y
+y(文史類).files\image114.png) =99
=99
y(文史類).files\image114.png) =9
=9
∴點P3的坐標可以為(3(文史類).files\image116.png) ,3).
,3).
(2)對每個自然數k,1≤k≤n,由題意(文史類).files\image118.png) 2=(k-1)d,及
2=(k-1)d,及
(文史類).files\image119.png) y
y(文史類).files\image121.png) =2pxk
=2pxk
,得x(文史類).files\image121.png) +2pxk=(k-1)d
+2pxk=(k-1)d
x(文史類).files\image121.png) +y
+y(文史類).files\image121.png) =(k-1)d
=(k-1)d
即(xk+p)2=p2+(k-1)d,
∴(x1+p)2, (x2+p)2, …,(xn+p)2是首項為p2,公差為d的等差數列.
(3)
【解法一】原點O到二次曲線C:(文史類).files\image122.png) (a>b>0)上各點的最小距離為b,最大距離為a.
(a>b>0)上各點的最小距離為b,最大距離為a.
∵a1=(文史類).files\image041.png) 2=a2, ∴d<0,且an=
2=a2, ∴d<0,且an=(文史類).files\image045.png) 2=a2+(n-1)d≥b2,
2=a2+(n-1)d≥b2,
∴(文史類).files\image124.png) ≤d<0. ∵n≥3,
≤d<0. ∵n≥3,(文史類).files\image126.png) >0
>0
∴Sn=na2+(文史類).files\image126.png) d在[
d在[(文史類).files\image127.png) ,0)上遞增,
,0)上遞增,
故Sn的最小值為na2+(文史類).files\image128.png) ?
?(文史類).files\image129.png) =
=(文史類).files\image131.png) .
.
【解法二】對每個自然數k(2≤k≤n),
由
x(文史類).files\image121.png) +y
+y(文史類).files\image121.png) =a2+(k-1)d
=a2+(k-1)d
,解得y(文史類).files\image121.png) =
=(文史類).files\image133.png)
(文史類).files\image135.png) +
+(文史類).files\image137.png) =1
=1
∵0< y(文史類).files\image121.png) ≤b2,得
≤b2,得(文史類).files\image139.png) ≤d<0 ∴
≤d<0 ∴(文史類).files\image140.png) ≤d<0
以下與解法一相同.
≤d<0
以下與解法一相同.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com