
題目列表(包括答案和解析)
函數f(x)的定義域為R,數列{an}滿足an=f(an-1)(n∈N*且n≥2).
(Ⅰ)若數列{an}是等差數列,a1≠a2,且f(an)-f(an-1)=k(an-an-1)(k為非零常數,n∈N*且n≥2),求k的值;
(Ⅱ)若f(x)=kx(k>1),a1=2,bn=lnan(n∈N*),數列{bn}的前n項和為Sn,對于給定的正整數m,如果![]() 的值與n無關,求k的值.
的值與n無關,求k的值.
設函數f ( x )的定義域、值域均為R,f ( x ) 反函數為f1 ( x ),且對任意實數x,均有f ( x ) + f1 ( x )<![]() 。定義數列{an} : a0 = 8 , a1 = 10 , an = f (an1 ) , n = 1, 2 , … .
。定義數列{an} : a0 = 8 , a1 = 10 , an = f (an1 ) , n = 1, 2 , … .
(1)求證:an+1 + an1<![]() an ( n = 1 , 2 , … ) ;
an ( n = 1 , 2 , … ) ;
(2)設![]() 求證:
求證:![]() ;
;
(3)是否存在常數A和B,同時滿足;
①當n = 0 及n = 1 時,有an =![]() 成立;
成立;
②當n = 2 , 3, … 時,有an<![]() 成立。
成立。
如果存在滿足上述條件的實數A、B的值;如果不存在,證明你的結論。
(1)求證:an+1 +an-1<![]() aN(N=1,2…).
aN(N=1,2…).
(2)設bN=an+1-2aN,N=0,1,2,….求證: bN<(-6)(![]() )n(N∈N*).
)n(N∈N*).
(3)是否存在常數A和B,同時滿足:
①當N=0及N=1時,有an=![]() 成立;
成立;
②當N=2,3…時,有an<![]() 成立.
成立.
如果存在滿足上述條件的實數A、B,求出A、B的值;如果不存在,證明你的結論.
(1)求證:an+1+an-1<![]() an(n=1,2,…);
an(n=1,2,…);
(2)設bn=an+1-2an,n=0,1,2,…,求證:bn<(-6)(![]() )n(n∈N*).
)n(n∈N*).
(3)是否存在常數A和B,同時滿足
①當n=0及n=1時,有an=![]() 成立;
成立;
②當n=2,3,…時,有an<![]() 成立.
成立.
如果存在滿足上述條件的實數A、B,求出A、B的值;如果不存在,證明你的結論.
函數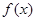 的定義域為
的定義域為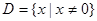 ,且滿足對于任意
,且滿足對于任意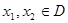 ,有
,有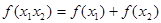 .
.
⑴求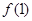 的值;
的值;
⑵判斷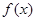 的奇偶性并證明;
的奇偶性并證明;
⑶如果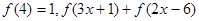 ≤
≤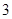 ,且
,且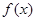 在
在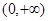 上是增函數,求
上是增函數,求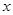 的取值范圍.
的取值范圍.
【解析】(Ⅰ) 通過賦值法,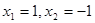 ,求出f(1)0;
,求出f(1)0;
(Ⅱ) 說明函數f(x)的奇偶性,通過令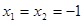 ,得
,得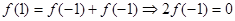 .令
.令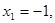
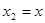 ,得
,得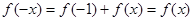 ,推出對于任意的x∈R,恒有f(-x)=f(x),f(x)為偶函數.
,推出對于任意的x∈R,恒有f(-x)=f(x),f(x)為偶函數.
(Ⅲ) 推出函數的周期,根據函數在[-2,2]的圖象以及函數的周期性,即可求滿足f(2x-1)≥12的實數x的集合.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com