題目列表(包括答案和解析)
本題有(1)．(2)．(3)三個選做題，每題7分，請考生任選2題作答，滿分14分．如果多做，則按所做的前兩題計分．作答時，先用2B鉛筆在答題卡上把所選題目對應的題號涂黑，并將所選題號填入括號中．
（1）(本小題滿分7分)選修4－2：矩陣與變換選做題
已知矩陣A=
有一個屬于特征值1的特征向量
.
(Ⅰ) 求矩陣A；
(Ⅱ) 矩陣B=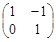
，點O(0,0)，M(2，-1)，N(0，2)，求
在矩陣AB的對應變換作用下所得到的
的面積.
（2）(本小題滿分7分)選修4－4：坐標系與參數方程選做題
在直角坐標平面內，以坐標原點O為極點，x軸的非負半軸為極軸建立極坐標系.已知曲線
的參數方程為
，曲線
的極坐標方程為
．
（Ⅰ）將曲線的參數方程化為普通方程；（Ⅱ）判斷曲線與曲線的交點個數，并說明理由．
（3）(本小題滿分7分)選修4－5：不等式選講選做題
已知函數
，不等式
在
上恒成立．
（Ⅰ）求
的取值范圍；
（Ⅱ）記的最大值為
，若正實數
滿足
，求
的最大值．
（A）將圓M：x2＋y2＝a（a＞0）的橫坐標伸長為原來的2倍，縱坐標縮短為原來的
，正好與直線x－y＝1相切，若以原點為極點，x軸非負半軸為極軸建立極坐標系，則圓M的極坐標方程為
（B）關于x的不等式：2－x2＞|x－a|至少有一個負數解，則實數a的取值范圍是
，正好與直線x－y＝1相切，若以原點為極點，x軸非負半軸為極軸建立極坐標系，則圓M的極坐標方程為 一、選擇題
題號
1
2
3
4
5
6
7
8
答案
A
C
B
D
A
B
A
B
1. A∵
∴
即
， 
，
∴
故選A；
C 
3 B 
4. D．由奇函數
可知
，而
，則
，當
時，
；當
時，
，又在
上為增函數，則奇函數在
上為增函數，
.
5 A 如圖知
是斜邊為3 的等腰直角三角形，
是直角邊為1等腰直角三角形，區域的面積
6. B 
，而
所以
，得
7. A 
，即
8. B
，所以解集為
，
又
，因此選B。
二、填空題
9. （－
，1）. 10. 
. 11. 
12. 
13. 
.
14. 
.
9. 
，
，
∴點M的直角坐標為（－，1）。
10.
11. 聯立解方程組
解得
，
即兩曲線的交點為
12. . ∴
，
13. . 
14. .依題意得
所以
，
三、解答題
15解：解法1：設矩形欄目的高為a cm，寬為b cm，則ab=9000. ①
廣告的高為a+20，寬為2b+25，其中a＞0，b＞0.
廣告的面積S＝(a+20)(2b+25)
＝2ab+40b+25a+500＝18500+25a+40b
≥18500+2
=18500+
當且僅當25a＝40b時等號成立，此時b=
,代入①式得a=120，從而b=75.
即當a=120，b=75時,S取得最小值24500.
故廣告的高為140 cm,寬為175 cm時，可使廣告的面積最小.
解法2：設廣告的高為寬分別為x cm，y cm，則每欄的高和寬分別為x－20，
其中x＞20，y＞25
兩欄面積之和為2(x－20)
,由此得y=
廣告的面積S=xy=x(
)＝x,
整理得S=
因為x－20＞0，所以S≥2
當且僅當
時等號成立，
此時有(x－20)2＝14400(x＞20)，解得x=140，代入y=
+25,得y＝175，
即當x=140，y＝175時，S取得最小值24500，
故當廣告的高為140 cm，寬為175 cm時，可使廣告的面積最小.
16. 證明：因為
為正實數，由平均不等式可得
即
所以
，
而
所以 
17. 解：（Ⅰ）
圖像如下：
（Ⅱ）不等式
，即
，
由
得
．
由函數圖像可知，原不等式的解集為
18.解：函數的定義域為
，且
19. （1）A
=
（2）
．
∴
20．解：對任意
,
,
,
,所以
,對任意的
，
，
，所以
0<
,令=
，
，
,所以
．
反證法:設存在兩個
使得
,
則
由
，得
，所以
，矛盾，故結論成立。
，所以
+…
．
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com