
本題有(1).(2).(3)三個選做題,每題7分,請考生任選2題作答,滿分14分.如果多做,則按所做的前兩題計分.作答時,先用2B鉛筆在答題卡上把所選題目對應的題號涂黑,并將所選題號填入括號中.
(1)(本小題滿分7分)選修4-2:矩陣與變換選做題
已知矩陣A= 有一個屬于特征值1的特征向量
有一個屬于特征值1的特征向量 .
.
(Ⅰ) 求矩陣A;
(Ⅱ) 矩陣B=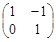 ,點O(0,0),M(2,-1),N(0,2),求
,點O(0,0),M(2,-1),N(0,2),求 在矩陣AB的對應變換作用下所得到的
在矩陣AB的對應變換作用下所得到的 的面積.
的面積.
(2)(本小題滿分7分)選修4-4:坐標系與參數方程選做題
在直角坐標平面內,以坐標原點O為極點,x軸的非負半軸為極軸建立極坐標系.已知曲線 的參數方程為
的參數方程為 ,曲線
,曲線 的極坐標方程為
的極坐標方程為 .
.
(Ⅰ)將曲線 的參數方程化為普通方程;(Ⅱ)判斷曲線
的參數方程化為普通方程;(Ⅱ)判斷曲線 與曲線
與曲線 的交點個數,并說明理由.
的交點個數,并說明理由.
(3)(本小題滿分7分)選修4-5:不等式選講選做題
已知函數 ,不等式
,不等式 在
在 上恒成立.
上恒成立.
(Ⅰ)求 的取值范圍;
的取值范圍;
(Ⅱ)記 的最大值為
的最大值為 ,若正實數
,若正實數 滿足
滿足 ,求
,求 的最大值.
的最大值.
(1)(Ⅰ) 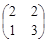 (Ⅱ)8 (2)(Ⅰ)
(Ⅱ)8 (2)(Ⅰ)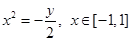 (Ⅱ)只有一個交點(3)(Ⅰ)
(Ⅱ)只有一個交點(3)(Ⅰ)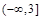 (Ⅱ)
(Ⅱ)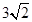
【解析】
試題分析:(1)(Ⅰ)由已知得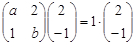 ,所以
,所以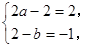 2分
2分
解得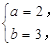 故A=
故A=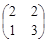 .3分.
.3分.
(Ⅱ)AB=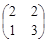
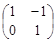 =
=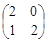 ,所以
,所以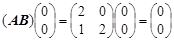 ,
,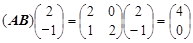 ,
,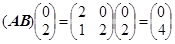 ,
5分
,
5分
即點O,M,N變成點O′(0,0),M′(4,0),N′(0,4),
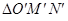 的面積為
的面積為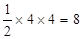 .
7分
.
7分
(2)(Ⅰ)由已知得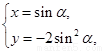 1分
1分
消去參數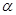 ,得
,得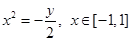 .
3分
.
3分
(Ⅱ)由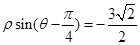 得曲線
得曲線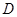 的直角坐標方程為
的直角坐標方程為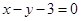 ,
4分
,
4分
由 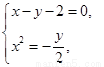 消去
消去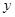 ,得
,得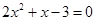 ,
5分
,
5分
解得 6分
6分
故曲線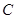 與曲線
與曲線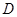 只有一個交點.
7分
只有一個交點.
7分
(3)(Ⅰ)因為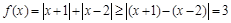 ,
,
所以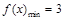 . 2分
. 2分
因為不等式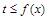 在R上恒成立,
在R上恒成立,
所以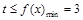 ,
, 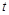 的取值范圍為
的取值范圍為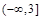 . 3分
. 3分
(Ⅱ)由(Ⅰ)得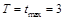 ,
,
由柯西不等式得: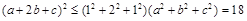 ,
,
所以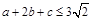 . 5分
. 5分
當且僅當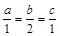 即
即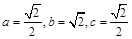 時,
時,
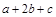 的最大值為
的最大值為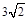 . 7分
. 7分
考點:矩陣極坐標及不等式性質
點評:三選一的題目一般難度不大,解極坐標問題常轉化為直角坐標,利用關系式
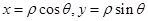 ,
,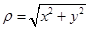 實現直角坐標與極坐標的互相轉化,絕對值不等式的求解結合絕對值的幾何意義可使計算簡化
實現直角坐標與極坐標的互相轉化,絕對值不等式的求解結合絕對值的幾何意義可使計算簡化


 學練快車道快樂假期暑假作業新疆人民出版社系列答案
學練快車道快樂假期暑假作業新疆人民出版社系列答案 浙大優學小學年級銜接導與練浙江大學出版社系列答案
浙大優學小學年級銜接導與練浙江大學出版社系列答案 小學暑假作業東南大學出版社系列答案
小學暑假作業東南大學出版社系列答案 津橋教育暑假拔高銜接廣東人民出版社系列答案
津橋教育暑假拔高銜接廣東人民出版社系列答案 波波熊暑假作業江西人民出版社系列答案
波波熊暑假作業江西人民出版社系列答案科目:高中數學 來源:2011屆福建省泉州外國語中學高三上學期期中考試數學理卷 題型:解答題
本題有(1)、(2)、(3)三個選答題,每題7分,請考生任選2題作答,滿分14分.如果多作,則按 所做的前兩題計分。作答時,先用2B鉛筆在答題卡上把所選題目對應的題號涂黑,并將選題號填入括號中
所做的前兩題計分。作答時,先用2B鉛筆在答題卡上把所選題目對應的題號涂黑,并將選題號填入括號中
(1)(本題滿分7分)選修4一2:矩陣與變換
求矩陣 的特征值及對應的特征向量。
的特征值及對應的特征向量。
(2)(本題滿分7分)選修4一4:坐標系與參數方程
已知直線 的參數方程:
的參數方程: (
( 為參數)和圓
為參數)和圓 的極坐標方程:
的極坐標方程: 。
。
(I)將直線 的參數方程化為普通方程,圓
的參數方程化為普通方程,圓 的極坐標方程化為直角坐標方程;
的極坐標方程化為直角坐標方程;
(II)判斷直線 和圓
和圓 的位置關系
的位置關系
(3)(本題滿分7分)選修4一5:不等式選講
已知函數 . 若不等式
. 若不等式
 恒成立,求實數
恒成立,求實數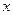 的范圍。
的范圍。
查看答案和解析>>
科目:高中數學 來源:2010-2011學年福建省高三上學期期中考試數學理卷 題型:解答題
本題有(1)、(2)、(3)三個選答題,每題7分,請考生任選2題作答,滿分14分.如果多作,則按 所做的前兩題計分。作答時,先用2B鉛筆在答題卡上把所選題目對應的題號涂黑,并將選題號填入括號中
所做的前兩題計分。作答時,先用2B鉛筆在答題卡上把所選題目對應的題號涂黑,并將選題號填入括號中
(1)(本題滿分7分)選修4一2:矩陣與變換
求矩陣 的特征值及對應的特征向量。
的特征值及對應的特征向量。
(2)(本題滿分7分)選修4一4:坐標系與參數方程
已知直線 的參數方程:
的參數方程: (
( 為參數)和圓
為參數)和圓 的極坐標方程:
的極坐標方程: 。
。
(I)將直線 的參數方程化為普通方程,圓
的參數方程化為普通方程,圓 的極坐標方程化為直角坐標方程;
的極坐標方程化為直角坐標方程;
(II)判斷直線 和圓
和圓 的位置關系
的位置關系
(3)(本題滿分7分)選修4一5:不等式選講
已知函數 . 若不等式
. 若不等式
 恒成立,求實數
恒成立,求實數 的范圍。
的范圍。
查看答案和解析>>
科目:高中數學 來源: 題型:
(本題滿分12分) 將一枚質地均勻且四個面上分別標有1,2,3,4的正四面體先
后拋擲兩次,其底面落于桌面上,記第一次朝下面的數字為![]() ,第二次朝下面的數
,第二次朝下面的數
字為![]() 。用
。用![]() 表示一個基本事件。
表示一個基本事件。
請寫出所有的基本事件;
求滿足條件“![]() 為整數”的事件的概率;
為整數”的事件的概率;
求滿足條件“![]() ”的事件的概率。
”的事件的概率。
查看答案和解析>>
科目:高中數學 來源: 題型:
本題有(1)、(2)、(3)三個選答題,每題7分,請考生任選2題作答,滿分14分.
1.(本小題滿分7分) 選修4一2:矩陣與變換
如果曲線![]()
![]() 在矩陣
在矩陣![]() 的作用下變換得到曲線
的作用下變換得到曲線![]() , 求
, 求![]() 的值。
的值。
2.(本小題滿分7分) 選修4一4:坐標系與參數方程
已知曲線![]() 的極坐標方程是
的極坐標方程是![]() ,直線
,直線![]() 的參數方程是
的參數方程是 (
(![]() 為參數).
為參數).
(1)將曲線![]() 的極坐標方程化為直角坐標方程;O
的極坐標方程化為直角坐標方程;O
(2)設直線![]() 與
與![]() 軸的交點是
軸的交點是![]() ,
,![]() 是曲線
是曲線![]() 上一動點,求
上一動點,求![]() 的最大值.
的最大值.
3.(本小題滿分7分)選修4-5:不等式選講
設函數![]()
(1)解不等式![]() ; (2)若
; (2)若![]() 的取值范圍。
的取值范圍。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com