題目列表(包括答案和解析)
（本題滿分12分）
對甲、乙兩種商品的重量的誤差進行抽查，測得數據如下(單位：
)：
甲：13 15 14 14 9 14 21 9 10 11
乙：10 14 9 12 15 14 11 19 22 16
（1）畫出樣本數據的莖葉圖，并指出甲，乙兩種商品重量誤差的中位數；
（2）計算甲種商品重量誤差的樣本方差；
（3）現從重量誤差不低于15的乙種商品中隨機抽取兩件，求重量誤差為19的商品被抽
中的概率。
（本題滿分12分）設{an}是等差數列，{bn}是各項都為正數的等比數列，且a1=b1=1，a3+b5=21，a5+b3=13.
(1)求{an}，{bn}的通項公式；
(2)求數列
的前n項和Sn.
（本題滿分12分）
對甲、乙兩種商品的重量的誤差進行抽查，測得數據如下(單位：
)：
甲：13 15 14 14 9 14 21 9 10 11
乙：10 14 9 12 15 14 11 19 22 16
（1）畫出樣本數據的莖葉圖，并指出甲，乙兩種商品重量誤差的中位數；
（2）計算甲種商品重量誤差的樣本方差；
（3）現從重量誤差不低于15的乙種商品中隨機抽取兩件，求重量誤差為19的商品被抽
中的概率。
（本題滿分12分）探究函數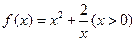
的最小值，并確定取得最小值時x的值. 列表如下, 請觀察表中y值隨x值變化的特點，完成以下的問題.
| x | … | 0.25 | 0.5 | 0.75 | 1 | 1.1 | 1.2 | 1.5 | 2 | 3 | 5 | … |
| y | … | 8.063 | 4.25 | 3.229 | 3 | 3.028 | 3.081 | 3.583 | 5 | 9.667 | 25.4 | … |
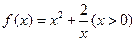在區間（0，1）上遞減，問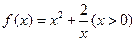：在區間 上遞增.當
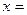時，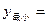
；
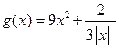在定義域內有最大值或最小值嗎？如有，是多少？此時x為何值？（直接回答結果，不需證明）（本題滿分12分）對甲、乙兩種商品的重量的誤差進行抽查，測得數據如下(單位：
)：
甲：13 15 14 14 9 14 21 9 10 11
乙：10 14 9 12 15 14 11 19 22 16
（1）畫出樣本數據的莖葉圖，并指出甲，乙兩種商品重量誤差的中位數；
（2）計算甲種商品重量誤差的樣本方差；
（3）現從重量誤差不低于15的乙種商品中隨機抽取兩件，求重量誤差為19的商品被抽中的概率。
1――12 A B B B B C D D C A C B
13、1 14、e 15、
16、①②④
17、解
在
上是增函數，
方程
=x2 + (m ? 2 )x + 1 = 0的兩個根在0至3之間
∴
∴
∴
＜m≤0
依題意得：m的取值范圍是:＜m≤-1或m＞0
18、解：（1）
,
當a=1時 解集為
當a>1時，解集為
，
當0<a<1時，解集為
；
（2）依題意知f(1)是f(x)的最小值，又f(1)不可能是端點值，則f(1)是f(x)的一個極小值，由
，
19、解：（1）當
所以f(-x)＝-(-x)2-(-x)+5=-x2+x+5，
所以f(x)=
（2）由題意，不妨設Ａ點在第一象限，坐標為(t,-t2-t+5)其中，
，
則S(t)=S ABCD=2t(-t2-t+5)=-2t3-2t2+10t.
，
令
得
（舍去），t2=1.
當
時
，所以S(t)在
上單調遞增，在
上單調遞減，
所以當t=1時，ABCD的面積取得極大值也是S(t)在上的最大值。
從而當t=1時，矩形ABCD的面積取得最大值6.
20、解：
21、解：
，
令
，要使
在其定義域內為單調函數，只需
在內滿足：
或
恒成立.
① 當
時，
，∵
，∴
，∴
，
∴在內為單調遞減.
② 當
時，，對稱軸為
， ∴
.
只需
，即
時，
，
∴在內為單調遞增。
③當
時，，對稱軸為
.
只需
，即
時在恒成立.
綜上可得，或.
22、解：（Ⅰ）
同理，令
∴f(x)單調遞增區間為
，單調遞減區間為
.
由此可知
（Ⅱ）由（I）可知當
時，有
，
即
.
.
（Ⅲ） 設函數
∴函數
）上單調遞增，在
上單調遞減.
∴的最小值為
，即總有
而
即
令
則
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com