
題目列表(包括答案和解析)
 某大學高等數學老師上學期分別采用了A,B兩種不同的教學方式對甲、乙兩個大一新生班進行教改試驗(兩個班人數均為60人,入學數學平均分數和優秀率都相同;勤奮程度和自覺性都一樣).現隨機抽取甲、乙兩班各20名同學的上學期數學期末考試成績,得到莖葉圖如圖:
某大學高等數學老師上學期分別采用了A,B兩種不同的教學方式對甲、乙兩個大一新生班進行教改試驗(兩個班人數均為60人,入學數學平均分數和優秀率都相同;勤奮程度和自覺性都一樣).現隨機抽取甲、乙兩班各20名同學的上學期數學期末考試成績,得到莖葉圖如圖:| 甲班 | 乙班 | 合計 | |
| 優秀 | |||
| 不優秀 | |||
| 合計 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
(本題滿分12分)將數字![]() 分別寫在大小、形狀都相同的
分別寫在大小、形狀都相同的![]() 張卡片上,將它們反扣后(數字向下),再從左到右隨機的依次擺放,然后從左到右依次翻卡片:若第一次就翻出數字
張卡片上,將它們反扣后(數字向下),再從左到右隨機的依次擺放,然后從左到右依次翻卡片:若第一次就翻出數字![]() 則停止翻卡片;否則就繼續翻,若將翻出的卡片上的數字依次相加所得的和是
則停止翻卡片;否則就繼續翻,若將翻出的卡片上的數字依次相加所得的和是![]() 的倍數則停止翻卡片;否則將卡片依次翻完也停止翻卡片.設翻卡片停止時所翻的次數為隨機變量
的倍數則停止翻卡片;否則將卡片依次翻完也停止翻卡片.設翻卡片停止時所翻的次數為隨機變量![]() ,求出
,求出![]() 的分布列和它的數學期望.
的分布列和它的數學期望.
(本小題滿分12分)
某大學高等數學老師上學期分別采用了 兩種不同的教學方式對甲、乙兩個大一新生班進行教改試驗(兩個班人數均為60人,入學數學平均分數和優秀率都相同;勤奮程度和自覺性都一樣)。現隨機抽取甲、乙兩班各20名同學的上學期數學期末考試成績,得到莖葉圖如下:
兩種不同的教學方式對甲、乙兩個大一新生班進行教改試驗(兩個班人數均為60人,入學數學平均分數和優秀率都相同;勤奮程度和自覺性都一樣)。現隨機抽取甲、乙兩班各20名同學的上學期數學期末考試成績,得到莖葉圖如下:

(Ⅰ)依莖葉圖判斷哪個班的平均分高?
(Ⅱ)從乙班這20名同學中隨機抽取兩名高等數學成績不得低于85分的同學,求成績為90分的同學被抽中的概率;
(Ⅲ)學校規定:成績不低于85分的為優秀,請填寫下面的 列聯表,并判斷“能否在犯錯誤的概率不超過0.025的前提下認為成績優秀與教學方式有關?”
列聯表,并判斷“能否在犯錯誤的概率不超過0.025的前提下認為成績優秀與教學方式有關?”
|
|
甲班 |
乙班 |
合計 |
|
優秀 |
|
|
|
|
不優秀 |
|
|
|
|
合計 |
|
|
|
下面臨界值表僅供參考:
|
|
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
|
|
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(參考公式: 其中
其中 )
)
(Ⅳ)從乙班高等數學成績不低于85分的同學中抽取2人,成績不低于90分的同學得獎金100元,否則得獎金50元,記 為這2人所得的總獎金,求
為這2人所得的總獎金,求 的分布列和數學期望。
的分布列和數學期望。
(本小題滿分12分)
某大學高等數學老師上學期分別采用了 兩種不同的教學方式對甲、乙兩個大一新生班進行教改試驗(兩個班人數均為60人,入學數學平均分數和優秀率都相同;勤奮程度和自覺性都一樣)。現隨機抽取甲、乙兩班各20名同學的上學期數學期末考試成績,得到莖葉圖如下:
兩種不同的教學方式對甲、乙兩個大一新生班進行教改試驗(兩個班人數均為60人,入學數學平均分數和優秀率都相同;勤奮程度和自覺性都一樣)。現隨機抽取甲、乙兩班各20名同學的上學期數學期末考試成績,得到莖葉圖如下:
(Ⅰ)依莖葉圖判斷哪個班的平均分高?
(Ⅱ)從乙班這20名同學中隨機抽取兩名高等數學成績不得低于85分的同學,求成績為90分的同學被抽中的概率;
(Ⅲ)學校規定:成績不低于85分的為優秀,請填寫下面的 列聯表,并判斷“能否在犯錯誤的概率不超過0.025的前提下認為成績優秀與教學方式有關?”
列聯表,并判斷“能否在犯錯誤的概率不超過0.025的前提下認為成績優秀與教學方式有關?”
| | 甲班 | 乙班 | 合計 |
| 優秀 | | | |
| 不優秀 | | | |
| 合計 | | | |
 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 其中
其中 )
)  為這2人所得的總獎金,求
為這2人所得的總獎金,求 的分布列和數學期望。
的分布列和數學期望。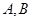 兩種不同的教學方式對甲、乙兩個大一新生班進行教改試驗(兩個班人數均為60人,入學數學平均分數和優秀率都相同;勤奮程度和自覺性都一樣)。現隨機抽取甲、乙兩班各20名同學的上學期數學期末考試成績,得到莖葉圖如下:
兩種不同的教學方式對甲、乙兩個大一新生班進行教改試驗(兩個班人數均為60人,入學數學平均分數和優秀率都相同;勤奮程度和自覺性都一樣)。現隨機抽取甲、乙兩班各20名同學的上學期數學期末考試成績,得到莖葉圖如下:
 列聯表,并判斷“能否在犯錯誤的概率不超過0.025的前提下認為成績優秀與教學方式有關?”
列聯表,并判斷“能否在犯錯誤的概率不超過0.025的前提下認為成績優秀與教學方式有關?”| | 甲班 | 乙班 | 合計 |
| 優秀 | | | |
| 不優秀 | | | |
| 合計 | | | |
 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 其中
其中 )
)  為這2人所得的總獎金,求
為這2人所得的總獎金,求 的分布列和數學期望。
的分布列和數學期望。
說明:
一、本解答指出了每題要考查的主要知識和能力,并給出了一種或幾種解法供參考,如果考生的解法與本解答不同,可根據試題的主要考查內容比照評分標準制定相應的評分細則.
二、對計算題,當考生的解答在某一步出現錯誤時,如果后繼部分的解答未改變該題的內容和難度,可視影響的程度決定后繼部分的給分,但不得超過該部分正確解答應給分數的一半;如果后繼部分的解答有較嚴重的錯誤,就不再給分.
三、解答右端所注分數,表示考生正確做到這一步應得的累加分數.
四、只給整數分數,選擇題和填空題不給中間分.
一、選擇題:本題考查基本知識和基本運算,每小題5分,滿分50分.
1. B 2. C 3. B 4.C 5.D 6.A 7. B 8. A 9. C 10. C
二、填空題:本題考查基本知識和基本運算,每小題4分,滿分20分.
11. 1 12.  13.
2 14.
13.
2 14.  15.
①③
15.
①③
三、解答題:本大題共6小題,共80分,解答應寫出文字說明,證明過程或演算步驟.
16. 本題主要考查三角函數的倍角公式、兩角和公式等基本知識,考查學生的運算求解能
力. 滿分13分.
解:(Ⅰ)因為 ,
,
兩邊同時平方得
 .
………………………………………(4分)
.
………………………………………(4分)
又 ,
,
所以 .
………………………………………(6分)
.
………………………………………(6分)
(Ⅱ)因為 ,
, ,
,
所以 ,得
,得 .
.
又 ,知
,知 . …………………(9分)
. …………………(9分)


 . ………………………………………(13分)
. ………………………………………(13分)
 17. 本題主要考查線線位置關系,二面角的求法等基本知識,考查空間想像能力,運算求解能力和推理論證能力. 滿分13分.
17. 本題主要考查線線位置關系,二面角的求法等基本知識,考查空間想像能力,運算求解能力和推理論證能力. 滿分13分.
解:(Ⅰ)證明:連結 ,
,
 側棱
側棱 底面ABC,
底面ABC,
 ,又
,又 .
.
 平面
平面 .
.
又 平面
平面 ,
,
 . ………(3分)
. ………(3分)
 ,
,
 四邊形
四邊形 為正方形,
為正方形,
 .
.
 ,
,  平面
平面 .
.
又 平面
平面 ,
, . …………(6分)
. …………(6分)
(Ⅱ)
 .
.

 平面
平面 .
.
又 ,
,  .
.
如圖,以 為原點,建立空間直角坐標系
為原點,建立空間直角坐標系 -xyz,設AP=x,則
-xyz,設AP=x,則

 、
、 、
、 、
、 .
.
知面 的一個法向量為
的一個法向量為 , ……(9分)
, ……(9分)
設面 的一個法向量為
的一個法向量為 ,
,
 ,
,
 .
.
由 得
得
令 ,
,  ………(11分)
………(11分)
依題意: =
=
解得 (不合題意,舍去),
(不合題意,舍去),
 時,二面角
時,二面角 的大小為
的大小為 . …………(13分)
. …………(13分)
18.本題主要考查數列與不等式等基本知識,考查運用數學知識分析問題與解決問題的能力,
考查應用意識. 滿分13分.
解:設第一年(今年)的汽車總量為 ,第n年的汽車總量為
,第n年的汽車總量為 ,則
,則

 ,
,
…
 .
.
數列 構成的首項為80000,公差為2000的等差數列,
構成的首項為80000,公差為2000的等差數列,
 . ………………………(4分)
. ………………………(4分)
若洗車行A從今年開始經過n年可以收回購買凈化設備的成本. 則( )
) -20000n≥900000,………………………(8分)
-20000n≥900000,………………………(8分)
整理得,

因為 ,所以
,所以  .
.
答:至少要經過6年才能收回成本. …………………………………………(13分)
19.本題主要考查直線與拋物線的位置關系、等比數列求和等基本知識,考查運算求解能力和分析問題、解決問題的能力. 滿分13分
解:(Ⅰ)依題意得: ,解得
,解得 .
.
所以拋物線方程為 . ………………………………………………(3分)
. ………………………………………………(3分)
(Ⅱ)若 ,即直線AB垂直于x軸,不防設
,即直線AB垂直于x軸,不防設 ,
,
由 又由拋物線對稱性可得:
又由拋物線對稱性可得: .
.
又 ,得
,得  ,故S△ABD=
,故S△ABD= . …………………………(4分)
. …………………………(4分)
若 ,設直線AB方程:
,設直線AB方程: ,
,
由方程組 消去
消去 得:
得: .(※)
.(※)
依題意可知: .
.
由已知得 ,
, . ……………………………………(5分)
. ……………………………………(5分)
由 ,得
,得 ,
,
即 ,整理得
,整理得 .
.
所以 . …………………………………………(6分)
. …………………………………………(6分)
 中點
中點 ,
,
所以點 ,
,
依題意知 .
.
又因為方程(※)中判別式 ,得
,得 .
.
所以 ,又
,又 ,
,
所以 .
.
又 為常數,故
為常數,故 的面積為定值. …………………………………(9分)
的面積為定值. …………………………………(9分)
(Ⅲ)依題意得:
 …,
…, .
.
故
 …
…

 <
< . ………………………………(13分)
. ………………………………(13分)
注:本題第(Ⅱ)問另解,參照本標準給分;第(Ⅲ)問若用定積分證明,同樣給分.
20. 本題主要考查函數的單調性、極值、最值、不等式等基本知識,考查運用導數研究函數
性質的方法,考查分類與整合及化歸與轉化等數學思想. 滿分14分.
解:(Ⅰ)依題意,知 的定義域為
的定義域為 .
.
當 時,
時, ,
, .
.
令 ,解得
,解得 .
.
當 時,
時, ;當
;當 時,
時, .
.
又 ,
,
所以 的極小值為
的極小值為 ,無極大值 . …………………………(3分)
,無極大值 . …………………………(3分)
(Ⅱ)
 .
.
令 ,解得
,解得 . …………………………(4分)
. …………………………(4分)
若 ,令
,令 ,得
,得 ;令
;令 ,得
,得 .
.
若 ,
,
①當 時,
時, ,
,
令 ,得
,得 或
或 ;
;
令 ,得
,得 .
.
②當 時,
時, .
.
③當 時,得
時,得 ,
,
令 ,得
,得 或
或 ;
;
令 ,得
,得 .
.
綜上所述,當 時,
時, 的遞減區間為
的遞減區間為 ,遞增區間為
,遞增區間為 .
.
當 時,
時, 的遞減區間為
的遞減區間為 ;遞增區間為
;遞增區間為 .
.
當 時,
時, 遞減區間為
遞減區間為 .當
.當 時,
時, 的遞減區間為
的遞減區間為 ,遞增區間為
,遞增區間為 . …………………………(9分)
. …………………………(9分)
(Ⅲ)當 時,
時, ,
,
由 ,知
,知 時,
時, .
.  ,
, .
.
依題意得: 對一切正整數成立. ……………(11分)
對一切正整數成立. ……………(11分)
令 ,則
,則 (當且僅當
(當且僅當 時取等號).
時取等號).
又 在區間
在區間 單調遞增,得
單調遞增,得 ,
,
故 ,又
,又 為正整數,得
為正整數,得 ,
,
當 時,存在
時,存在 ,
, ,
,
對所有 滿足條件.
滿足條件.
所以,正整數 的最大值為32. …………………………………(14分)
的最大值為32. …………………………………(14分)
21. (1)本題主要考查矩陣乘法與變換等基本知識,考查運算求解能力,考查函數與方程思
想. 滿分7分.
解:PQ= ,
,
PQ矩陣表示的變換T: 滿足條件
滿足條件
 .
.
所以 ………………………(3分)
………………………(3分)
直線 任取點
任取點 ,則點
,則點 在直線
在直線 上,
上,
故 ,又
,又 ,得
,得
所以 ………………………………………(7分)
………………………………………(7分)
(2)本題主要考查直線極坐標方程和橢圓參數方程等基本知識,考查運算求解能力,考查化歸與轉化思想. 滿分7分.
解:由題意知直線和橢圓方程可化為:
 , ①
, ①
 . ② …………………………(2分)
. ② …………………………(2分)
①②聯立,消去 得:
得: ,解得
,解得 ,
, .
.
設直線與橢圓交于A、B兩點,則

 .
.
故所求的弦長為 . &n
. &n
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com