
題目列表(包括答案和解析)
設(shè)正數(shù)列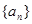 的前
的前 項(xiàng)和為
項(xiàng)和為 ,且
,且 .
.
(1)求數(shù)列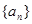 的首項(xiàng)
的首項(xiàng) ;
;
(2)求數(shù)列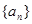 的通項(xiàng)公式;
的通項(xiàng)公式;
(3)設(shè)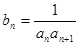 ,
, 是數(shù)列
是數(shù)列 的前
的前 項(xiàng)和,求使得
項(xiàng)和,求使得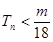 對(duì)所有
對(duì)所有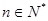 都成立的最小正整數(shù)
都成立的最小正整數(shù) .
.
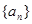 的前
的前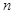 項(xiàng)和為
項(xiàng)和為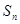 ,且
,且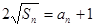 .
.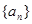 的首項(xiàng)
的首項(xiàng)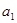 ;
;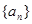 的通項(xiàng)公式;
的通項(xiàng)公式;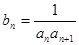 ,
,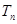 是數(shù)列
是數(shù)列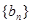 的前
的前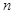 項(xiàng)和,求使得
項(xiàng)和,求使得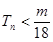 對(duì)所有
對(duì)所有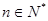 都成立的最小正整數(shù)
都成立的最小正整數(shù)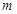 .
.設(shè)正數(shù)列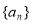 的前
的前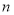 項(xiàng)和為
項(xiàng)和為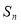 ,且
,且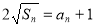 .
.
(1)求數(shù)列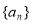 的首項(xiàng)
的首項(xiàng)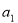 ;
;
(2)求數(shù)列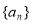 的通項(xiàng)公式;
的通項(xiàng)公式;
(3)設(shè)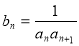 ,
,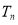 是數(shù)列
是數(shù)列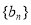 的前
的前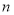 項(xiàng)和,求使得
項(xiàng)和,求使得 對(duì)所有
對(duì)所有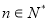 都成立的最小正整數(shù)
都成立的最小正整數(shù)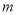 .
.
設(shè) 是數(shù)列
是數(shù)列 的前
的前 項(xiàng)和,對(duì)任意
項(xiàng)和,對(duì)任意 都有
都有 成立, (其中
成立, (其中 、
、 、
、 是常數(shù)).
是常數(shù)).
(1)當(dāng) ,
, ,
, 時(shí),求
時(shí),求 ;
;
(2)當(dāng) ,
, ,
, 時(shí),
時(shí),
①若 ,
,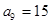 ,求數(shù)列
,求數(shù)列 的通項(xiàng)公式;
的通項(xiàng)公式;
②設(shè)數(shù)列 中任意(不同)兩項(xiàng)之和仍是該數(shù)列中的一項(xiàng),則稱(chēng)該數(shù)列是“
中任意(不同)兩項(xiàng)之和仍是該數(shù)列中的一項(xiàng),則稱(chēng)該數(shù)列是“ 數(shù)列”.
數(shù)列”.
如果 ,試問(wèn):是否存在數(shù)列
,試問(wèn):是否存在數(shù)列 為“
為“ 數(shù)列”,使得對(duì)任意
數(shù)列”,使得對(duì)任意 ,都有
,都有
 ,且
,且 .若存在,求數(shù)列
.若存在,求數(shù)列 的首項(xiàng)
的首項(xiàng) 的所
的所
有取值構(gòu)成的集合;若不存在,說(shuō)明理由.
設(shè)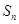 是數(shù)列
是數(shù)列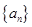 的前
的前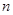 項(xiàng)和,對(duì)任意
項(xiàng)和,對(duì)任意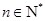 都有
都有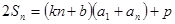 成立, (其中
成立, (其中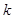 、
、 、
、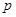 是常數(shù)).
是常數(shù)).
(1)當(dāng)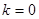 ,
,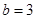 ,
,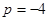 時(shí),求
時(shí),求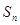 ;
;
(2)當(dāng)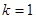 ,
,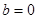 ,
,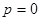 時(shí),
時(shí),
①若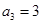 ,
,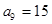 ,求數(shù)列
,求數(shù)列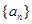 的通項(xiàng)公式;
的通項(xiàng)公式;
②設(shè)數(shù)列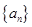 中任意(不同)兩項(xiàng)之和仍是該數(shù)列中的一項(xiàng),則稱(chēng)該數(shù)列是“
中任意(不同)兩項(xiàng)之和仍是該數(shù)列中的一項(xiàng),則稱(chēng)該數(shù)列是“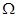 數(shù)列”.
數(shù)列”.
如果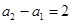 ,試問(wèn):是否存在數(shù)列
,試問(wèn):是否存在數(shù)列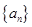 為“
為“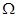 數(shù)列”,使得對(duì)任意
數(shù)列”,使得對(duì)任意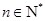 ,都有
,都有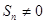 ,且
,且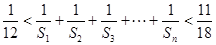 .若存在,求數(shù)列
.若存在,求數(shù)列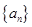 的首項(xiàng)
的首項(xiàng)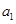 的所
的所
有取值構(gòu)成的集合;若不存在,說(shuō)明理由.
福州八中2006級(jí)高中數(shù)學(xué)選修4-2模塊考試
一、選擇題 BDAC
二、填空題
|