題目列表(包括答案和解析)
已知f(x)＝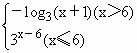
，若記f－1(x)為f(x)的反函數，且a＝f－1(
)，則f(a＋4)＝________．
已知f(x)是定義在R上的偶函數，且對任意
，都有f(x－1)＝f(x＋3)，當
[4，6]時，f(x)＝2x＋1，則函數f(x)在區間[－2，0]上的反函數f－1(x)的值f－1(19)為
A．log215
B．3－2log23
C．5＋log23
D．－1－2log23
已知定義在R上的函數f(x)同時滿足條件：(1)f(0)＝2；(2)f(x)＞1，且
；當x∈R時，f′(x)＞0．若f(x)的反函數是f－1(x)，則不等式f－1(x)＜0的解集為
A．(0，2)
B．(1，2)
C．(－∞，2)
D．(2,＋∞)
已知函數f(x)＝ax(a＞0，且a≠1)的反函數為y＝f－1(x)，若f－1(2)＋f－1(5)＝1，則a等于________．
CBACA;DCADC;DB
30;9,27;1; 
17. 解:易得
………… 3分
當a＝1時， B＝
，滿足
；
………… 5分
當
時，B＝{x|即B
A，
必須
，解之得
………… 8分
綜上可知，存在這樣的實數a
滿足題設成立. ………… 10分
18. 解: (1) 圖2是由四塊圖1所示地磚繞點
按順時針旋轉
后得到，△
為等腰直角三角形，
四邊形
是正方形.
……
4分
(2) 設
，則
，每塊地磚的費用為
，制成△、△
和四邊形
三種材料的每平方米價格依次為
. …… 10分
由
，當
時，有最小值，即總費用為最省.
答：當
米時，總費用最省. …… 12分
19. 解:(Ⅰ)易得
，
的解集為
，
恒成立.
解得
.………………… 3分
因此
的對稱軸
， 故函數在區間
上不單調，從而不存在反函數。
……………………… 5分
(Ⅱ)由已知可得
，則
,
令
得
.
………………………7分
①
若
，則
在上單調遞增，在
上無極值;
②
若
，則當
時，
；當
時，
.
當
時，
有極小值
在區間上存在極小值，
.
③
若
，則當
時，；當
時，.
當
時，有極小值.
在區間上存在極小值 
.……………… 10分
綜上所述：當
時，在區間上存在極小值。………… 12分
20. 解:(Ⅰ)當
時,
故
,即數列的通項公式為
…… 4分
(Ⅱ)當
時,
當
…… 8分
由此可知,數列
的前n項和
為
…… 12分
21. 解:(Ⅰ)
.
…… 4分
(Ⅱ)易得的值域為A＝
，設函數的值域B，若對于任意
總存在
，使得
成立，只需
。
…… 6分
顯然當
時，
，不合題意；
當
時，
，故應有
，解之得：
；…… 8分
當
時，
，故應有
，解之得：
。…… 10分
綜上所述，實數
的取值范圍為
。
…… 12分
22. 解:(Ⅰ)
.
…… 3分
(Ⅱ) 
…… 6分
，
由錯位相減法得：
，
所以：
。 …… 8分
(Ⅲ) 
為遞增數列 。
中最小項為
…… 12分
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com