
題目列表(包括答案和解析)
(本小題滿分10分)
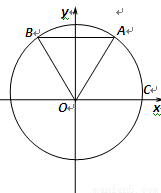
如圖: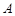 、
、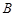 是單位圓
是單位圓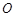 上的點,
上的點,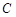 是圓與
是圓與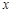 軸正半軸的交點,三角形
軸正半軸的交點,三角形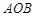 為正三角形, 且AB∥
為正三角形, 且AB∥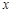 軸.
軸.
(1)求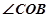 的三個三角函數值;
的三個三角函數值;
(2)求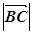 及
及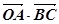 .
.
(本小題滿分10分)
如圖: 、
、 是單位圓
是單位圓 上的點,
上的點, 是圓與
是圓與 軸正半軸的交點,三角形
軸正半軸的交點,三角形 為正三角形, 且AB∥
為正三角形, 且AB∥ 軸.
軸.
(1)求 的三個三角函數值;
的三個三角函數值;
(2)求 及
及 .
.
 、
、 是單位圓
是單位圓 上的點,
上的點, 是圓與
是圓與 軸正半軸的交點,三角形
軸正半軸的交點,三角形 為正三角形, 且AB∥
為正三角形, 且AB∥ 軸.
軸.
 的三個三角函數值;
的三個三角函數值; 及
及 .
.(本小題滿分10分)
某企業生產A、B兩種產品,根據市場調查和預測,A產品的利潤與投資成正比,其關系如圖1,B產品的利潤與投資的算術平方根成正比,其關系如圖2(注:利潤與投資單位是萬元)

(1)分別將A、B兩種產品的利潤表示為投資的函數,并寫出它們的函數關系式;
(2)該企業已籌集到10萬元資金,并全部投入A、B兩種產品的生產,問:怎樣分配這10萬元投資,才能使企業獲得最大利潤,其最大利潤為多少萬元?

1.B 2.B 3.A 4.C 5.C 6.B 7.D 8.B 9.C 10.B
11.A 12.D
【解析】
1.,所以選B.
2.的系數是,所以選B.
3.,所以選.
4.為鈍角或,所以選C
5.,所以選C.
6.,所以選B.
7.,所以選D.
8.化為或,所以選B.
9.將左移個單位得,所以選A.
10.直線與橢圓有公共點,所以選B.
11.如圖,設,則,
,
,從而,因此與底面所成角的正弦值等于.所以選A.
12.畫可行域 可知符合條件的點是:共6個點,故,所以選D.
二、
13.185..
14.60..
15.,由,得
.
16..如圖:
如圖,可設,又,
.
當面積最大時,.點到直線的距離為.
三、
17.(1)由三角函數的定義知:.
(2)
.
18.(1)設兩年后出口額恰好達到危機前出口額的事件為,則.
(2)設兩年后出口額超過危機前出口額的事件為,則.
19.(1)設與交于點.
從而,即,又,且
平面為正三角形,為的中點,
,且,因此,平面.
(2)平面,∴平面平面又,∴平面平面
設為的中點,連接,則,
平面,過點作,連接,則.
為二面角的平面角.
在中,.
又.
20.(1)
(2)
又
綜上:.
21.(1)的解集為(1,3)
∴1和3是的兩根且
由此得
時,時,
在處取得極小值
③
由式①、②、③聯立得:
.
(2)
∴當時,在上單調遞減,
當時,
當時,在[2,3]上單調遞增,
22.(1)由得
∴橢圓的方程為:.
(2)由得,
又
設直線的方程為:
由得
由此得. ①
設與橢圓的交點為,則
由得
,整理得
,整理得
時,上式不成立, ②
由式①、②得
或
∴取值范圍是.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com