
題目列表(包括答案和解析)
在函數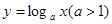 的圖象上有
的圖象上有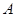 、
、 、
、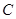 三點,橫坐標分別為
三點,橫坐標分別為 其中
其中 .
.
⑴求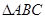 的面積
的面積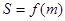 的表達式;
的表達式;
⑵求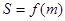 的值域.
的值域.
【解析】由題意利用分割可先表示三角形ABC的面積,然后應用對數運算性質及二次函數的性質求解函數的最大值,屬于知識的簡單綜合.
如圖,四棱柱 中,
中,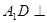 平面
平面 ,底面
,底面 是邊長為
是邊長為 的正方形,側棱
的正方形,側棱 .
.

(1)求三棱錐 的體積;
的體積;
(2)求直線 與平面
與平面 所成角的正弦值;
所成角的正弦值;
(3)若棱 上存在一點
上存在一點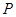 ,使得
,使得 ,當二面角
,當二面角 的大小為
的大小為 時,求實數
時,求實數 的值.
的值.
【解析】(1)在 中,
中,
 .
(3’)
.
(3’)
(2)以點D為坐標原點,建立如圖所示的空間直角坐標系 ,則
,則
 (4’)
(4’)
 ,設平面
,設平面 的法向量為
的法向量為 ,
,
由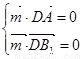 得
得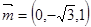 ,
(5’)
,
(5’)
則 ,
,
 . (7’)
. (7’)
(3)
設平面 的法向量為
的法向量為 ,由
,由 得
得 ,
(10’)
,
(10’)

已知曲線 的參數方程是
的參數方程是 (
( 是參數),以坐標原點為極點,
是參數),以坐標原點為極點, 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線 :的極坐標方程是
:的極坐標方程是 =2,正方形ABCD的頂點都在
=2,正方形ABCD的頂點都在 上,且A,B,C,D依逆時針次序排列,點A的極坐標為(2,
上,且A,B,C,D依逆時針次序排列,點A的極坐標為(2, ).
).
(Ⅰ)求點A,B,C,D的直角坐標;
(Ⅱ)設P為 上任意一點,求
上任意一點,求 的取值范圍.
的取值范圍.
【命題意圖】本題考查了參數方程與極坐標,是容易題型.
【解析】(Ⅰ)由已知可得 ,
, ,
,
 ,
, ,
,
即A(1, ),B(-
),B(- ,1),C(―1,―
,1),C(―1,― ),D(
),D( ,-1),
,-1),
(Ⅱ)設 ,令
,令 =
= ,
,
則 =
= =
= ,
,
∵ ,∴
,∴ 的取值范圍是[32,52]
的取值范圍是[32,52]
已知數列 是各項均不為0的等差數列,公差為d,
是各項均不為0的等差數列,公差為d, 為其前n項和,且滿足
為其前n項和,且滿足 ,
, .數列
.數列 滿足
滿足 ,
, ,
, 為數列
為數列 的前n項和.
的前n項和.
(1)求數列 的通項公式
的通項公式 和數列
和數列 的前n項和
的前n項和 ;
;
(2)若對任意的 ,不等式
,不等式 恒成立,求實數
恒成立,求實數 的取值范圍;
的取值范圍;
(3)是否存在正整數
 ,使得
,使得 成等比數列?若存在,求出所有
成等比數列?若存在,求出所有 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
【解析】第一問利用在 中,令n=1,n=2,
中,令n=1,n=2,
得 即
即
解得 ,,
,, [
[
又 時,
時, 滿足
滿足 ,
,
 ,
,

第二問,①當n為偶數時,要使不等式 恒成立,即需不等式
恒成立,即需不等式 恒成立.
恒成立.
 ,等號在n=2時取得.
,等號在n=2時取得.
 此時
此時 需滿足
需滿足 .
.
②當n為奇數時,要使不等式 恒成立,即需不等式
恒成立,即需不等式 恒成立.
恒成立.
 是隨n的增大而增大, n=1時
是隨n的增大而增大, n=1時 取得最小值-6.
取得最小值-6.
 此時
此時 需滿足
需滿足 .
.
第三問 ,
,
若 成等比數列,則
成等比數列,則 ,
,
即. 
由 ,可得
,可得 ,即
,即 ,
,
 .
. 
(1)(法一)在 中,令n=1,n=2,
中,令n=1,n=2,
得 即
即
解得 ,,
,, [
[
又 時,
時, 滿足
滿足 ,
,
 ,
,
 .
.
(2)①當n為偶數時,要使不等式 恒成立,即需不等式
恒成立,即需不等式 恒成立.
恒成立.
 ,等號在n=2時取得.
,等號在n=2時取得.
 此時
此時 需滿足
需滿足 .
.
②當n為奇數時,要使不等式 恒成立,即需不等式
恒成立,即需不等式 恒成立.
恒成立.
 是隨n的增大而增大, n=1時
是隨n的增大而增大, n=1時 取得最小值-6.
取得最小值-6.
 此時
此時 需滿足
需滿足 .
.
綜合①、②可得 的取值范圍是
的取值范圍是 .
.
(3) ,
,
若 成等比數列,則
成等比數列,則 ,
,
即. 
由 ,可得
,可得 ,即
,即 ,
,
 .
. 
又 ,且m>1,所以m=2,此時n=12.
,且m>1,所以m=2,此時n=12.
因此,當且僅當m=2,
n=12時,數列 中的
中的 成等比數列
成等比數列
如圖,直線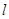 與拋物線
與拋物線 交于
交于 兩點,與
兩點,與 軸相交于點
軸相交于點 ,且
,且 .
.
(1)求證: 點的坐標為
點的坐標為 ;
;
(2)求證: ;
;
(3)求 的面積的最小值.
的面積的最小值.

【解析】設出點M的坐標 ,并把過點M的方程設出來.為避免對斜率不存在的情況進行討論,可以設其方程為
,并把過點M的方程設出來.為避免對斜率不存在的情況進行討論,可以設其方程為 ,然后與拋物線方程聯立消x,根據
,然后與拋物線方程聯立消x,根據 ,即可建立關于
,即可建立關于 的方程.求出
的方程.求出 的值.
的值.
(2)在第(1)問的基礎上,證明: 即可.
即可.
(3)先建立面積S關于m的函數關系式,根據 建立即可,然后再考慮利用函數求最值的方法求最值.
建立即可,然后再考慮利用函數求最值的方法求最值.
1. 構造向量 ,
, ,所以
,所以 ,
, .由數量積的性質
.由數量積的性質 ,得
,得 ,即
,即 的最大值為2.
的最大值為2.
2. ∵ ,令
,令 得
得 ,所以
,所以 ,當
,當 時,
時, ,當
,當 時,
時, ,所以當
,所以當 時,
時, .
.
3.∵ ,∴
,∴ ,
, ,又
,又 ,∴
,∴ ,則
,則 ,所以周期
,所以周期 .作出
.作出 在
在 上的圖象知:若
上的圖象知:若 ,滿足條件的
,滿足條件的 (
( )存在,且
)存在,且 ,
, 關于直線
關于直線 對稱,
對稱, ,
, 關于直線
關于直線 對稱,∴
對稱,∴ ;若
;若 ,滿足條件的
,滿足條件的 (
( )存在,且
)存在,且 ,
, 關于直線
關于直線 對稱,
對稱, ,
, 關于直線
關于直線 對稱,
對稱,
 ∴
∴ .
.
4. 不等式 (
( )表示的區域是如圖所示的菱形的內部,
)表示的區域是如圖所示的菱形的內部,
∵
 ,
,
當 ,點
,點 到點
到點 的距離最大,此時
的距離最大,此時 的最大值為
的最大值為 ;
;
當 ,點
,點 到點
到點 的距離最大,此時
的距離最大,此時 的最大值為3.
的最大值為3.
5. 由于已有兩人分別抽到5和14兩張卡片,則另外兩人只需從剩下的18張卡片中抽取,共有 種情況.抽到5 和14的兩人在同一組,有兩種情況:
種情況.抽到5 和14的兩人在同一組,有兩種情況:
(1) 5 和14 為較小兩數,則另兩人需從15~20這6張中各抽1張,有 種情況;
種情況;
(2) 5 和14 為較大兩數,則另兩人需從1~4這4張中各抽1張,有 種情況.
種情況.
于是,抽到5 和14 兩張卡片的兩人在同一組的概率為 .
.
 6. ∵
6. ∵ ,∴
,∴ ,
,
設 ,
, ,則
,則 .
.
作出該不等式組表示的平面區域(圖中的陰影部分 ).
).
令 ,則
,則 ,它表示斜率為
,它表示斜率為 的一組平行直線,易知,當它經過點
的一組平行直線,易知,當它經過點 時,
時, 取得最小值.
取得最小值.
解方程組 ,得
,得 ,∴
,∴
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com