
題目列表(包括答案和解析)
(本小題滿分14分)
已知橢圓C的中心在坐標原點,焦點在x軸上,它的一個頂點恰好是拋物線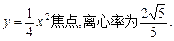
(1) 求橢圓C的標準方程;
(2)過橢圓C的右焦點F作直線l交橢圓C于A、B兩點,交y軸于M點,若 求
求 的值.
的值.
(本小題滿分14分)
已知橢圓C的中心在原點,焦點在 軸上,以兩個焦點和短軸的兩個端點
軸上,以兩個焦點和短軸的兩個端點
為頂點的四邊形是一個面積為8的正方形(記為Q).
(Ⅰ)求橢圓C的方程;
(Ⅱ)設點P是橢圓C的左準線與 軸的交點,過點P的直線
軸的交點,過點P的直線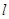 與橢圓C相交于M,N兩點,當線段MN的中點落在正方形Q內(包括邊界)時,求直線
與橢圓C相交于M,N兩點,當線段MN的中點落在正方形Q內(包括邊界)時,求直線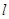 的斜率的取值范圍。
的斜率的取值范圍。
(本小題滿分14分)
已知橢圓C的中心在坐標原點,焦點在x軸上,它的一個頂點恰好是拋物線
(1) 求橢圓C的標準方程;
(2)過橢圓C的右焦點F作直線l交橢圓C于A、B兩點,交y軸于M點,若 求
求 的值.
的值.
(本小題滿分14分)
已知橢圓C的左,右焦點坐標分別為![]() ,離心率是
,離心率是![]() 。橢圓C的左,右頂點分別記為A,B。點S是橢圓C上位于
。橢圓C的左,右頂點分別記為A,B。點S是橢圓C上位于![]() 軸上方的動點,直線AS,BS與直線
軸上方的動點,直線AS,BS與直線![]() 分別交于M,N兩點。
分別交于M,N兩點。
求橢圓C的方程;
求線段MN長度的最小值;
當線段MN的長度最小時,在橢圓C上的T滿足:T到直線AS的距離等于![]() .
.
試確定點T的個數。
(本小題滿分14分)
已知橢圓C的焦點F1(-![]() ,0)和F2(
,0)和F2(![]() ,0),長軸長6,設直線
,0),長軸長6,設直線![]() 交橢圓C于A、B兩點,求線段AB的中點坐標。
交橢圓C于A、B兩點,求線段AB的中點坐標。
一、1.B 2.B 3.D 4.B 5.D 6.A 7.B 8.C 9.B 10.B 11.B 12.D
二、13. 14.32 15.162 16.3
三、17.解:(1)
(2)
,
18.解:(1)設5次實驗中只成功一次為事件A,一次都不成功為事件B,
則P(5次實驗至少2次成功)=1-P(A)-P(B)=1-
(法2:所求概率為)
(2)ξ的可能取值為2、3、4、5
又
19.解法1:(1)取CD的中點E,連結PE、EM、EA
∵△PCD為正三角形 ∴PE⊥CD,PE=PDsin∠PDE=2sin60°=
∵平面PCD⊥平面ABCD ∴PE⊥平面ABCD
∵四邊形ABCD是矩形 ∴△ADE、△ECM、△ABM均為直角三角形
由勾股定理可求得EM=,AM=,AE=3 ∴EM2+AM2=AE2
∴∠AME=90° ∴AM⊥PM
(2)由(1)可知EM⊥AM,PM⊥AM ∴∠PME是二面角P―AM―D的平面角
∴tan∠PME= ∴∠PMA=45° ∴二面角P―AM―D為45°
(3)設D點到平面PAM的距離為d,連結DM,則
在Rt△PEM中,由勾股定理可求得PM=,,
解法2:(1)以D點為原點,
分別以直線DA、DC
為x軸、y軸,建立
如圖所示的空間直角
坐標系D―xyz,
依題意,可得D(0,0,0),P(0,1,),C(0,2,0),A(2,0,0),
M(,2,0),
即,∴AM⊥PM.
(2)設平面PAM,則
取y=1,得 顯然平面ABCD
.
結合圖形可知,二面角P―AM―D為45°;
(3)設點D到平面PAM的距離為d,由(2)可知)與平面PAM垂直,
則
即點D到平面PAM的距離為
20.解:(1)
①當時 由
解得:定義域為(0,+∞)
∴函數的單調遞增區間為(
由可知的單調遞增區間為
②當時 同理可得:函數的單調遞增區間為
函數的單調遞減區間為
(2)當時,
令
當上單調遞增
當上單調遞減
又在[1,3]上連續 為函數的極大值.
又
是函數在[1,3]上的最小值,
為在[1,3]的最大值.
21.解:(1)在直線
∵P1為直線l與y軸的交點,∴P1(0,1) ,
又數列的公差為1
(2)
(3)
是以2為公比,4為首項的等比數列,
22.解:(1)直線l過點(3,)且方向向量為)
∴l方程為 化簡為:
∵直線和橢圓交于兩點和x軸交于M(1,0)
又
即
(2) ∴橢圓C方程為
由
∴橢圓C方程為:
(3)將中得 ①
由韋達定理知:
由②2/③知:………④
對方程①求判別式,且由 即
化簡為:………………⑤
由④式代入⑤式可知:,求得,
又橢圓的焦點在x軸上,則,
由④知:,結合,求得
因此所求橢圓長軸長2a范圍為(2,).
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com