
題目列表(包括答案和解析)
已知橢圓的中心在原點、焦點在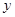 軸上, 若其離心率是
軸上, 若其離心率是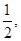 焦距是8,則該橢圓的方程
焦距是8,則該橢圓的方程
為
已知橢圓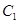 的中心在原點、焦點在
的中心在原點、焦點在 軸上,拋物線
軸上,拋物線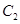 的頂點在原點、焦點在
的頂點在原點、焦點在 軸上.小明從曲線
軸上.小明從曲線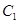 、
、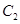 上各取若干個點(每條曲線上至少取兩個點),并記錄其坐標(
上各取若干個點(每條曲線上至少取兩個點),并記錄其坐標(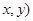 .由于記錄失誤,使得其中恰有一個點既不在橢圓
.由于記錄失誤,使得其中恰有一個點既不在橢圓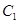 上,也不在拋物線
上,也不在拋物線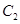 上,小明的記錄如下:
上,小明的記錄如下:
 | 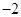 | 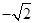 |  |  | 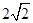 |  |
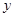 |  |  | 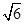 | 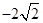 | 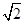 | 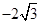 |
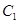 的方程為
的方程為 已知橢圓的中心在原點、焦點在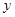 軸上, 若其離心率是
軸上, 若其離心率是 焦距是8,則該橢圓的方程
焦距是8,則該橢圓的方程
為
 的中心在原點、焦點在
的中心在原點、焦點在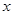 軸上,拋物線
軸上,拋物線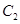 的頂點在原點、焦點在
的頂點在原點、焦點在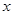 軸上.小明從曲線
軸上.小明從曲線 、
、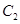 上各取若干個點(每條曲線上至少取兩個點),并記錄其坐標(
上各取若干個點(每條曲線上至少取兩個點),并記錄其坐標(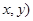 .由于記錄失誤,使得其中恰有一個點既不在橢圓
.由于記錄失誤,使得其中恰有一個點既不在橢圓 上,也不在拋物線
上,也不在拋物線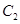 上,小明的記錄如下:
上,小明的記錄如下: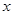 |  |  |  |  |  |  |
 |  |  |  |  |  |  |
 的方程為
的方程為 已知橢圓的中心在原點、焦點在![]() 軸上,若其離心率是
軸上,若其離心率是![]() ,焦距是8,則該橢圓的方程為 ▲ .
,焦距是8,則該橢圓的方程為 ▲ .
一、選擇題:
1.B 2.C 3.D 4.C 5. B 6.A 7. C 8.A 9.A 10. B 11.B 12. A
二、填空題:
13. .files/image250.gif) 14.
14. .files/image252.gif) ∪
∪.files/image254.gif) 15.
15. .files/image256.gif) 16.
16. .files/image258.gif)
17. 360 18. .files/image260.gif) 19.
19. .files/image262.gif) ∪
∪.files/image264.gif) 20.1320 21.2/5
22.5 23. 9/8 24. 正四面體內任意一點到各個面的距離之和等于此正四面體的高 25.5/7 26.
20.1320 21.2/5
22.5 23. 9/8 24. 正四面體內任意一點到各個面的距離之和等于此正四面體的高 25.5/7 26..files/image266.gif)
三、解答題:
27解:(I).files/image268.gif)
.files/image270.gif)
.files/image272.gif)
.files/image274.gif)
.files/image276.gif)
.files/image278.gif)
(II)由.files/image280.gif) 得
得.files/image282.gif)
.files/image284.gif)
.files/image286.gif)
.files/image288.gif)
.files/image290.gif) 的x的取值范圍是
的x的取值范圍是.files/image292.gif)
28解:(1)甲隊以二比一獲勝,即前兩場中甲勝1場,第三場甲獲勝,其概率為
.files/image294.gif)
(2)乙隊以2:0獲勝的概率為.files/image296.gif) ;
;
乙隊以2:1獲勝的概率為.files/image298.gif)
∴乙隊獲勝的概率為P2=P'2+P''2=0.16+0.192=0.352.
29解:(1)
|